La présence d'un champ local 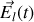va causer une mise en mouvement partielle des charges liées et donc engendrer un courant.

Par exemple dans le cas de l'atome d'hydrogène le moment dipolaire vaut

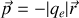
où 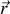est la position de l'électron et 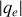sa charge. Si la répartition des dipôles est uniforme, avec 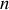la densité, le vecteur polarisation vaut

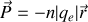
alors que par définition le courant 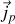associé aux charges de polarisation vaut

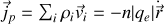
par conséquent

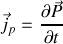
Nous pouvons vérifier que cette expression est en accord avec la loi de conservation de la charge. En effet comme

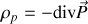
la divergence de l'expression précédente donne

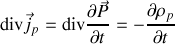
ce qui vérifie bien la conservation de la charge.