Nous avions établi que les molécules polaires avaient tendance à orienter leur dipôle dans le sens du champ électrique local afin de minimiser l'énergie potentielle, cette tendance étant contrariée par l'agitation thermique.

Cependant, si on supprime instantanément le champ local, on constate que la dépolarisation des molécules n'est pas instantanée. Debye a introduit l'équation différentielle du premier ordre suivante pour modéliser le phénomène de relaxation de la polarisation :

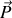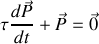
avec une solution en

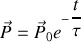
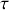étant un temps de relaxation qui a pour valeur typique 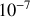s . En présence d'un champ local l'équation devient

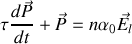
ce qui entraîne que pour les temps longs la polarisation tend vers la valeur statique .

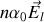On admettra que cette équation reste valable pour un champ 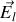dépendant du temps par exemple sous la forme

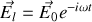
Si 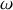est petit devant l'orientation des dipôles suit sans retard l'orientation du champ et la polarisabilité sera proche de la valeur statique.

Si ces valeurs sont comparables il apparaîtra un déphasage entre la polarisation et le champ local.

Si enfin 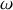est très grand devant les oscillations du champ étant trop rapide, les dipôles n'auront pas le temps de s'orienter et la polarisabilité tendra vers 0.

Quantitativement en introduisant une polarisation complexe

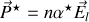
l'équation différentielle en régime forcé établi donne

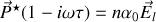
d'où

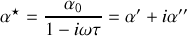
d'où

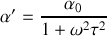
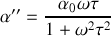
Par conséquent on voit bien que 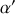décroît avec la fréquence en partant de la valeur statique et tend vers 0, alors que 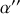partant de 0 présente un maximum pour 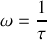et tend ensuite vers 0.