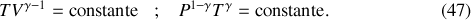Pour une transformation adiabatique quasi-statique, la variation d'entropie est nécessairement nulle. Des équations (36) et (41) découlent alors les deux égalités différentielles :
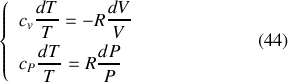
En combinant ces égalités et en introduisant le coefficient de Laplace
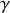(soit le rapport de
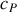à
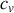, nécessairement plus grand que un), il vient :
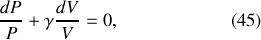
et, par intégration directe, la Loi de Laplace vérifiée par un gaz parfait sur n'importe quel chemin adiabatique réversible :
Remarque :
La Loi de Laplace peut être exprimée en fonction des variables
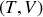ou
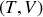grâce à la loi du gaz parfait (27). Par substitution de
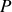ou de
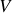, il vient directement :
