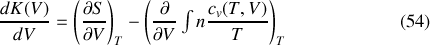Considérons tout d'abord le cas particulier d'un corps 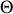de très grande capacité thermique relativement à la quantité d'énergie qu'il est susceptible d'échanger par chaleur. Le corps peut alors être assimilé à un thermostat. Sa température restant constante au cours de l'échange, il vient :

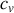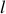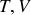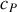Pour un corps dont la température est au contraire susceptible de varier au cours d'un échange thermique, le calcul analytique n'est pas toujours possible. Si toutefois son équation d'état est connue, les relations de Clapeyron permettent de calculer les fonctions et pour un choix de variables ( ), ou et 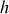pour un choix de variables ( 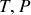). Pour le choix ( 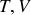), par exemple, la différentielle de l'entropie s'écrit formellement :

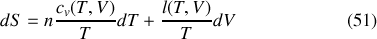
Cependant, à la différence des cas idéaux du gaz parfait et du corps incompressible, les dérivées partielles de l'entropie dépendent en général des deux variables d'intégration choisies :

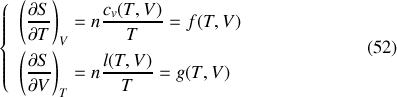
Pour intégrer la différentielle, il faut alors procéder en deux étapes :

• intégrer par rapport à l'une des deux variables dont dépend la différentielle. Le point délicat est que la "constante d'intégration'' dépend a priori de l'autre variable :

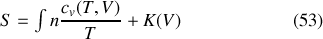
• dériver l'expression obtenue par rapport à la deuxième variable, puis identifier cette dérivée avec la dérivée partielle de 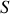par rapport à cette dernière variable. Cela permet de déterminer la dérivée de la pseudo-constante 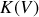, et, par intégration ultérieure, la variation d'entropie du système.