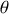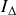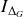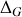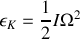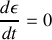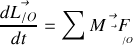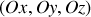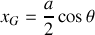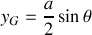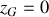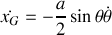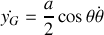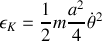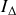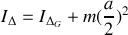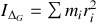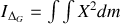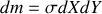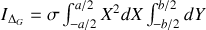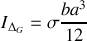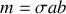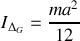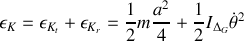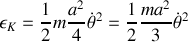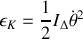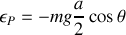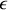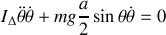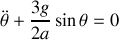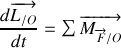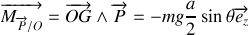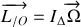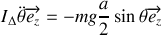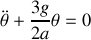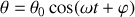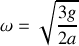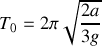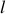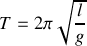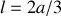Cinématique et dynamique du solide - Etude d'un pendule composé

Cinématique et dynamique du solide

Etude d'un pendule composé

Énoncé

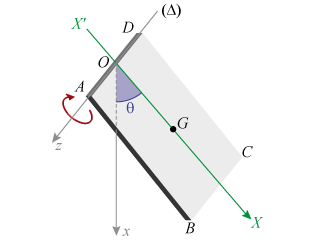
Un pendule pesant mobile autour d'un axe horizontal 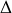( 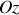) est constitué d'une plaque solide rectangulaire 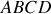, de masse 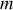, d'épaisseur 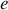constante que l'on supposera négligeable devan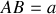t et 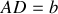Toute cause de frottement sera également négligée. désigne un axe vertical orienté positivement vers le bas. On posera .

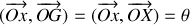Quel est le nombre de degrés de liberté de ce pendule et les coordonnées permettant de décrire le mouvement de la plaque ?
Quelles sont les coordonnées du centre de masse ainsi que son vecteur vitesse ? En déduire l'énergie cinétique correspondant au mouvement de translation du pendule.
Donner le vecteur rotation 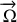autour de son axe de rotation et de n'importe quel axe parallèle à ce dernier.
Calculer le moment d'inertie par rapport à l'axe .
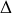Quelle est l'énergie cinétique totale due au mouvement de la plaque ? Montrer que c'est une rotation pure par rapport à un axe que l'on précisera.
Quelle est l'énergie potentielle de la plaque ? A partir de l'énergie mécanique totale, déduire les équations du mouvement.
Appliquer le théorème du moment cinétique en 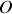pour retrouver l'équation du mouvement.
Dans l'approximation des petits angles, intégrer l'équation du mouvement et en déduire la période 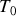des oscillations. Quelle est, en fonction de 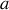, la longueur du pendule simple synchrone ?

Aide simple

Solution détaillée

figure

Ce pendule ne présente qu'un degré de liberté. L'angle sera utilisé pour décrire le mouvement.
Dans le repère

Vitesse du centre d'inertie:

D'où pour l'énergie cinétique associée à ce mouvement:
Il s'agit d'une rotation d'angle autour de l'axe ,
Pour calculer , utilisons le théorème de Huygens et le moment d'inertie , l'axe étant parallèle à et passant par .

avec

comme ,
d'où,
Le centre d'inertie est animé d'un mouvement de translation et de rotation

ce qui revient à considérer un mouvement de rotation pure autour de l'axe puisque
Seule l'énergie potentielle de pesanteur intervient ici avec
Le système est conservatif puisque les frottements sont négligés, l'énergie mécanique est conservée soit

ce qui donne l'équation différentielle suivante:
Appliquons le théorème du moment cinétique en :

La plaque est soumise au poids ainsi qu'aux forces de liaison selon l'axe . la droite d'action des forces de liaison interceptant l'axe de rotation, seul le poids contribue au moment.

, ayant été explicité en 3.,
soit
On retrouve l'équation différentielle établie précédemment.
Dans l'approximation des petits angles, d'où l'équation différentielle suivante:
la solution sera de la forme caractérisant un mouvement oscillant de pulsation
La période de ce pendule vaut donc à comparer avec la période d'un pendule simple de longueur ,
Le pendule simple synchrone , i.e. ayant la même fréquence d'oscillation, sera constitué d'un fil d'une longueur et d'une masse ponctuelle quelconque.