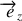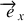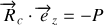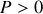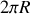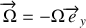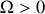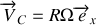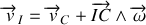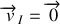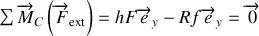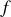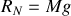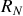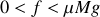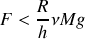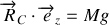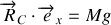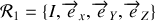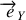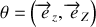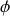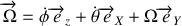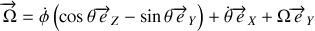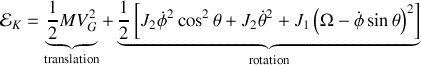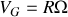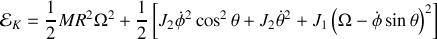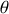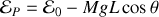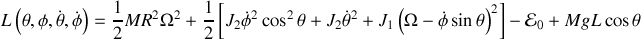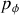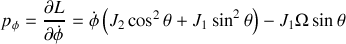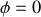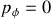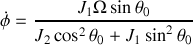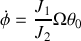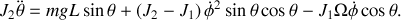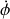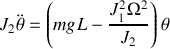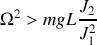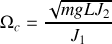Lors d'un roulement sans glissement le centre
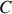 de la roue se déplace d'une longueur
de la roue se déplace d'une longueur
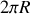 quand la roue fait un tour. On note
quand la roue fait un tour. On note
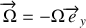 avec
avec
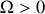 la vitesse de rotation de la roue par rapport au sol. La vitesse du point
la vitesse de rotation de la roue par rapport au sol. La vitesse du point
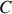 lors d'un roulement sans glissement vaut par conséquent
lors d'un roulement sans glissement vaut par conséquent
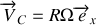 . Examinons maintenant la vitesse au point
. Examinons maintenant la vitesse au point
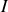 :
:
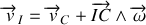
Nous voyons alors que le roulement sans glissement impose
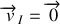 .
.
On note
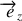 un vecteur unitaire vertical ascendant et
un vecteur unitaire vertical ascendant et
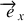 un vecteur unitaire horizontal dont la direction correspond au sens de déplacement du vélo.
un vecteur unitaire horizontal dont la direction correspond au sens de déplacement du vélo.
Le non-glissement impose que la somme des moments des forces extérieures appliquées à la roue soit nulles, empêchant ainsi la roue de tourner sur elle-même en glissant sur le sol. Le plus simple est de calculer la somme des moments des forces au point
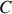 , ainsi la réaction du cadre sur la roue ne contribue pas. Il y a roulement sans glissement si :
, ainsi la réaction du cadre sur la roue ne contribue pas. Il y a roulement sans glissement si :
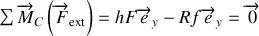
où
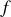 est la force de frottement de la roue sur le sol. Comme il n'y a pas de mouvement dans la direction verticale, la somme des forces extérieurs est nulle dans cette direction et l'on obtient:
est la force de frottement de la roue sur le sol. Comme il n'y a pas de mouvement dans la direction verticale, la somme des forces extérieurs est nulle dans cette direction et l'on obtient:
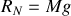 où
où
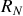 est la réaction normale du sol sur la roue. La force de frottement peut prendre des valeurs comprises entre
est la réaction normale du sol sur la roue. La force de frottement peut prendre des valeurs comprises entre
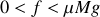 . Le roulement sans glissement impose donc :
. Le roulement sans glissement impose donc :
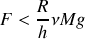 .
.
La roue exerce sur le cadre du vélo une force
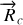 appliquée au point
appliquée au point
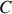 . Comme il y a équilibre dans la direction
. Comme il y a équilibre dans la direction
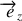 ,
,
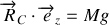 La composante horizontale du cadre sur la roue se déduit en faisant le bilan des forces horizontales :
La composante horizontale du cadre sur la roue se déduit en faisant le bilan des forces horizontales :
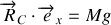
On introduit un repère cartésien
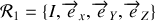 où
où
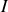 est le point de contact entre la roue et le sol, l'axe
est le point de contact entre la roue et le sol, l'axe
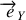 étant aligné avec l'axe de rotation de la roue. On définit l'angle d'inclinaison :
étant aligné avec l'axe de rotation de la roue. On définit l'angle d'inclinaison :
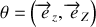 . On note
. On note
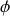 l'angle de rotation du mono-cycle dans le plan horizontal c'est-à-dire autour de l'axe
l'angle de rotation du mono-cycle dans le plan horizontal c'est-à-dire autour de l'axe
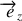 . Le vecteur rotation de la roue vaut :
. Le vecteur rotation de la roue vaut :
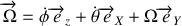 .
.
que l'on peut écrire dans les axes propres de la roue
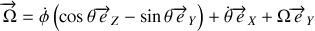 .
.
L'énergie cinétique du mono-cycle à la forme :
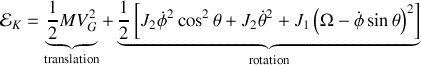
Comme il y a roulement sans glissement
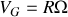 si bien que
si bien que
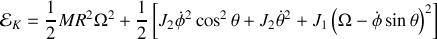 .
.
L'énergie potentiel ne dépend elle que de l'angle
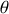 :
:
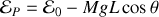 .
.
On en déduit le Lagrangien :
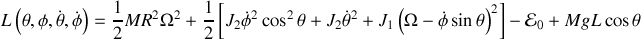
La coordonnée
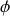 est cyclique et l'impulsion
est cyclique et l'impulsion
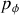 est une constante du mouvement :
est une constante du mouvement :
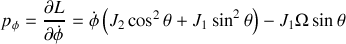 .
.
Cette impulsion est liée à la projection du moment cinétique dans la direction
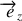 .
.
Plaçons nous maintenant dans le cas où le cycliste modifie l'angle
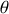 pour passer de la situation initiale
pour passer de la situation initiale
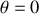 à la situation finale
à la situation finale
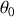 . Pour cela il impose à la roue un moment de rotation porté par l'axe
. Pour cela il impose à la roue un moment de rotation porté par l'axe
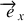 en déportant latéralement sont centre de gravité. Ce moment ne fait donc pas varier la quantité
en déportant latéralement sont centre de gravité. Ce moment ne fait donc pas varier la quantité
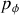 qui reste conservée. Or à l'instant initiale
qui reste conservée. Or à l'instant initiale
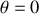 et
et
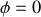 (le vélo roule en ligne droite) par conséquent,
(le vélo roule en ligne droite) par conséquent,
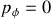 . Comme
. Comme
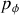 est une constante du mouvement, on a donc :
est une constante du mouvement, on a donc :
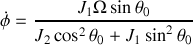
ce qui nous donne la vitesse de rotation du mono-cycle dans le plan.
Dans l'approximation des petits angles, on obtient :
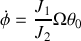
La vitesse de rotation augmente avec l'angle d'inclinaison, la vitesse de rotation de la roue et le rapport du moment axial au moment transverse.
Étudions maintenant la stabilité du mono-cycle en considérant l'angle
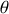 comme variable. Le système présente deux degrés de liberté
comme variable. Le système présente deux degrés de liberté
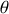 et
et
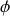 , l'équation pour
, l'équation pour
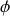 ayant déjà été déterminée, regardons l'équation pour l'angle
ayant déjà été déterminée, regardons l'équation pour l'angle
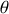 :
:
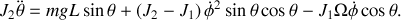
En se plaçant dans l'approximation des petits angles et en remplaçant
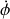 par l'expression déjà déterminée, il vient :
par l'expression déjà déterminée, il vient :
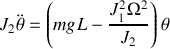 .
.
Le cycliste est donc en équilibre stable si
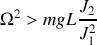 . La vitesse de rotation critique de stabilité
. La vitesse de rotation critique de stabilité
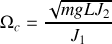 est d'autant plus faible que le centre de gravité du vélo est bas, et que le moment principal
est d'autant plus faible que le centre de gravité du vélo est bas, et que le moment principal
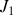 est important.
est important.
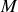 et d'une roue de vélo de centre
et d'une roue de vélo de centre
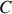 de masse négligeable et de rayon
de masse négligeable et de rayon
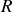 , roule sur une surface horizontale plane. On note
, roule sur une surface horizontale plane. On note
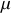 le coefficient de frottement cinématique entre la roue et le sol et
le coefficient de frottement cinématique entre la roue et le sol et
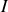 le point de contact entre la roue et le sol. On note
le point de contact entre la roue et le sol. On note
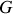 le centre de gravité du mono-cycle avec
le centre de gravité du mono-cycle avec
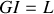 .
.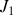 et les moments
et les moments
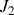 sur les axes transverses sont égaux. On néglige le moment d'inertie du cadre.
sur les axes transverses sont égaux. On néglige le moment d'inertie du cadre.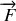 dont la droite d'action est à une distance
dont la droite d'action est à une distance
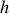 du centre de la roue
du centre de la roue
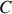 .
.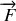
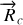 de la roue sur le cadre. En déduire l'accélération du mono-cycle
de la roue sur le cadre. En déduire l'accélération du mono-cycle .
.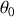 par rapport à la verticale dans la direction transverse du mouvement, on engendre une rotation de la roue dans le plan horizontale. On se placera dans le cas d'une faible inclinaison
par rapport à la verticale dans la direction transverse du mouvement, on engendre une rotation de la roue dans le plan horizontale. On se placera dans le cas d'une faible inclinaison
 .
.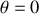 .
.