Énoncé
Considérons une toupie de symétrique de masse M, de centre d'inertie G, à la distance l de la pointe fixe O et soumise au champ de pesanteur.
Donner le vecteur rotation total.
Donner le lagrangien du système.
Quelles sont les coordonnées cycliques? En déduire les intégrales premières associées ainsi que les vitesses de rotation
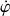et
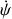.Écrire la conservation de l'énergie en fonction de
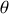, de la vitesse de rotation associée et des grandeurs conservées. Mettre cette équation sous la forme :
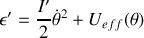avec
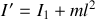.La condition énergie cinétique de rotation
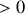permet de déduire les conditions limites sur
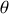. Montrer qu'un mouvement de nutation apparaît, lequel dépend du signe de la quantité (
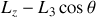).Une rotation stable autour de l'axe Oz correspond à
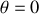et à un minimum de
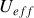. Quelle inégalité doit être vérifiée par
?
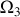1) Travailler avec les angles d'Euler (
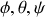) caractérisant respectivement la précession, la nutation et la rotation propre.
Les vecteurs vitesses de rotation s'ajoutent vectoriellement pour donner :
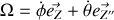
Écrire les composantes des vecteurs rotation dans le repère
.
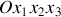2) La toupie est supposée symétrique,
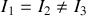
Pour la rotation,
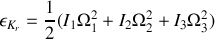
Pour la translation,
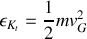
3)
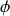et
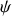sont des coordonnées cycliques puisque
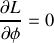et
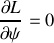
Elles sont associées aux intégrales premières suivantes :
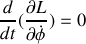et
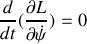
5) Écrire l'égalité vérifiée par
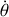et montrer que le signe
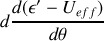dépend du signe de
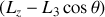
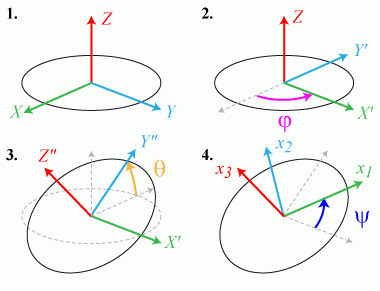
Distinguons la première rotation d'angle
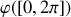autour de Z transformant OXYZ en OX'Y'Z,la 2de rotation d'angle
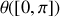autour de X' transformant OX'Y'Z en OX'Y''Z'',la 3ème rotation d'angle
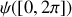autour de Z'' transformant OX'Y''Z'' en
.
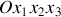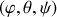sont les angles d'Euler caractérisant respectivement la précession, la nutation et la rotation propre. Les vecteurs vitesses de rotation s'ajoutent vectoriellement pour donner :
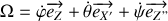
Écrivons les composantes des vecteurs rotation dans le repère
.
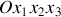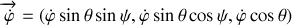
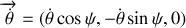
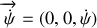.Le vecteur
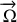représentant le mouvement de rotation complet s'écrit :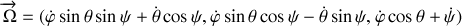
La toupie est supposée symétrique,
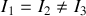. L'énergie cinétique de rotation s'écrit donc :
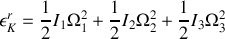. Le choix des directions des axes principaux d'inertie
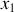et
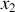est arbitraire pour une toupie symétrique.Choisissons
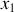tel que ON et
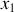coïncident, soit
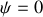mais
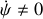.Dans ce cas, le vecteur rotation devient :
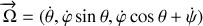
L'énergie cinétique de rotation s'écrit alors :
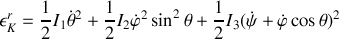
Le centre d'inertie a l'énergie cinétique de translation suivante :
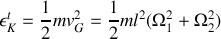
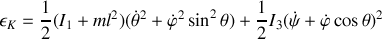
Il n'y a que l'énergie potentielle de pesanteur :
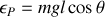
d'où le lagrangien,
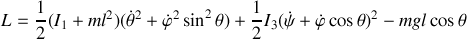
Posons
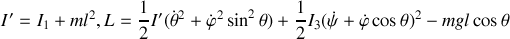
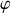et
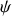sont des coordonnées cycliques puisque
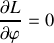et
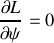
Elles sont associées aux intégrales premières suivantes :
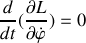
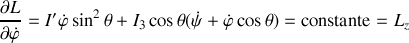
avec
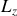, composante du moment cinétique de rotation défini par rapport à O et projeté suivant Oz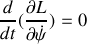
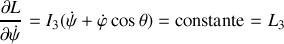
avec
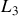, composante du moment cinétique de rotation défini par rapport à O et projeté suivant
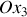
De ces 2 équations couplées , on déduit les vitesses angulaires
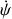et
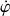en fonction de
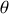et des constantes
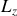et
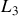
soit
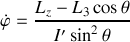
et
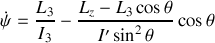
L'énergie totale s'écrit :
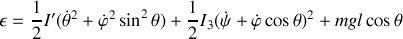
soit en remplaçant les vitesses angulaires
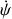et
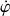par les expressions trouvées en 3) :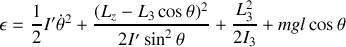 
Écrivons l'énergie sous la forme :
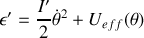
avec
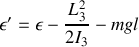
et
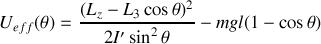
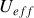représente un potentiel efficace pour l'étude du mouvement en
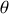
L'intégration de ces équations mènent à des intégrales elliptiques dont la résolution est très mathématique. On peut toutefois déterminer qualitativement les propriétés intéressantes de ce mouvement.
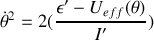donc
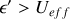
Pour que le mouvement existe, il faut que
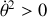c'est-à-dire que
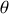est limité au domaine
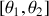.L'axe de symétrie de la toupie aura un angle
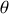par rapport à la vertical Oz qui oscillera entre
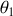et
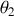. Il s'agit de la nutation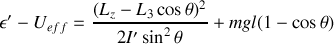
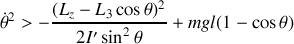
Le signe de
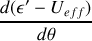dépend du signe de
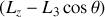
si
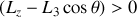pour tout le domaine de variation de
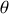entre
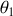et
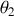, alors
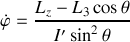ne change pas de signe. La précession est continue mais de vitesse variable (
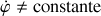).De même si
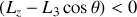pour tout le domaine de variation de
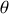entre
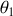et
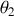.si (
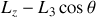) change de signe lorsque
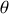varie entre
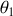et
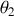. La fonction
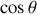est croissante monotone entre
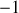et
,
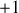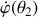aura le signe inverse de
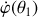. La précession continue mais l'axe décrit des boucles (mouvement de va-et-vient).si (
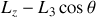) ne change pas de signe lorsque
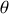varie entre
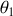et
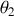mais s'annule soit à
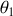soit à
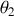, le mouvement de précession continue mais marque un temps d'arrêt lorsque la nutation atteint une la valeur limite où
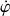s'annule. Par exemple,
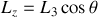en
.
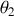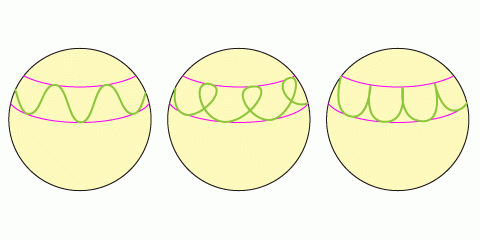
Les 3 cas de figures sont représentés en bas de page. La sphère représente l'espace que peut explorer l'extrémité libre de la toupie. La trajectoire réelle de la pointe libre est représentée sur cette sphère.
Lorsque la toupie est mise en mouvement avec un vitesse élevée et une faible inclinaison de l'axe par rapport à la verticale, l'axe demeure pratiquement vertical lors du mouvement jusqu'à ce que sa vitesse diminue et que le mouvement devienne instable.
À
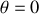, Oz et
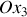coïncident,
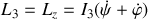
Effectuons un développement limité de
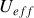au voisinage de
,
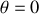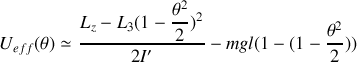
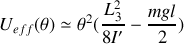
La position de la toupie est stable tant que
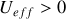, i.e.
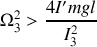. Si la friction diminue cette vitesse de rotation, le mouvement devient désordonné. Dans le cas d'une toupie rapide, l'énergie cinétique de sa rotation propre est beaucoup plus importante que l'énergie potentielle de pesanteur. Il y a compétition entre le terme de pesanteur qui tend à faire tomber la toupie et le terme en
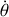du potentiel effectif qui tend au contraire à ramener l'axe de la toupie vers la verticale. À grande vitesse, le mouvement de la toupie à point fixe se rapproche du cas libre.
