Énoncé
Un cylindre
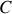 homogène de masse
homogène de masse
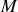 de rayon
de rayon
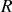 et de hauteur
et de hauteur
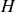 est mis en rotation avec une vitesse
est mis en rotation avec une vitesse
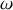 autour d'un axe
autour d'un axe
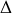 passant par le centre de gravité de
passant par le centre de gravité de
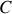 et incliné d'un angle
et incliné d'un angle
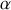 constant par rapport à l'axe de symétrie
constant par rapport à l'axe de symétrie
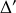 du cylindre. Calculer les moments des forces appliquées par l'axe
du cylindre. Calculer les moments des forces appliquées par l'axe
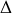 sur le bâti.
sur le bâti.
à compléter
Déterminer les trois moments d'inertie principaux du cylindre et les axes propres.
Décomposer le vecteur rotation du cylindre dans la base des axes propres du cylindre. En déduire l'énergie cinétique du cylindre.
En déduire le tenseur d'inertie du cylindre dans une base cartésienne dont l'un des axes est confondu avec l'axe de rotation
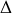 .
.
NLP_C_M02_G01
à compléter
On note
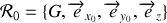 un repère cartésien fixe par rapport au sol d'origine le centre de gravité
un repère cartésien fixe par rapport au sol d'origine le centre de gravité
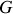 de
de
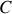 dont le vecteur
dont le vecteur
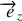 est aligné avec l'axe
est aligné avec l'axe
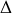 ,
,
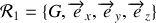 un repère cartésien fixe par rapport au cylindre d'origine
un repère cartésien fixe par rapport au cylindre d'origine
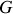 dont le vecteur
dont le vecteur
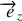 est aligné avec l'axe
est aligné avec l'axe
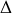 et
et
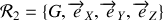 un repère cartésien fixe par rapport au cylindre d'origine
un repère cartésien fixe par rapport au cylindre d'origine
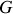 dont le vecteur
dont le vecteur
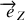 est aligné avec l'axe
est aligné avec l'axe
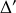 .
.
Les axes principaux du cylindre sont confondus avec les axe du repère
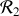 . Calculons les moments principaux d'inertie. Pour des raisons de symétrie, il est évident que
. Calculons les moments principaux d'inertie. Pour des raisons de symétrie, il est évident que
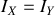 . Néanmoins le calcul est un peu long
. Néanmoins le calcul est un peu long
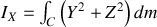
Pour mener le calcul, il faut découper le cylindre en ``tranches'' parallèles au plan
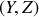 et d'épaisseur
et d'épaisseur
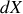 . Chaque tranche est un parallélépipède rectangle d'épaisseur
. Chaque tranche est un parallélépipède rectangle d'épaisseur
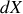 de longueur
de longueur
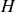 et de largeur
et de largeur
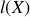 . La largeur
. La largeur
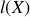 dépend de la position
dépend de la position
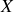 de la tranche dans le cylindre. Le calcul s'effectue en intégrant en premier lieu sur
de la tranche dans le cylindre. Le calcul s'effectue en intégrant en premier lieu sur
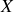 et
et
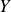 puis sur
puis sur
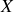 . Comme le cylindre est homogène, l'élément de masse
. Comme le cylindre est homogène, l'élément de masse
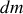 vaut
vaut
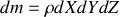 .
.
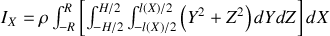
Or
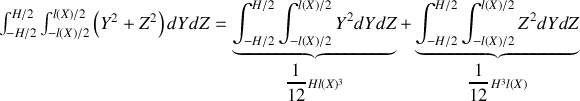
Soit
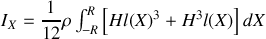
la largeur
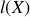 est la longueur d'une corde d'un cercle de rayon
est la longueur d'une corde d'un cercle de rayon
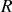 à une distance
à une distance
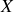 du centre du cercle, on en déduit la relation
du centre du cercle, on en déduit la relation
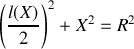 soit
soit
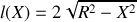
d'où
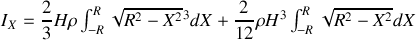
Les calculs se simplifient en posant
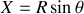 ainsi
ainsi
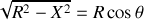 et
et
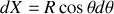 de sorte que :
de sorte que :
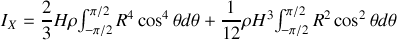
Pour calculer les intégrales, il faut linéariser les cosinus
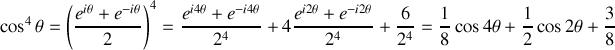
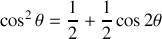
soit
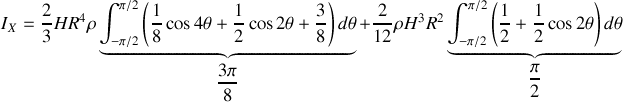
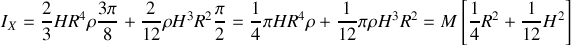
Le calcul de
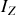 est plus rapide :
est plus rapide :
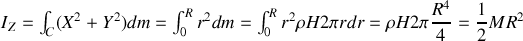
Le vecteur rotation
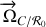 du cylindre par rapport au repère fixe
du cylindre par rapport au repère fixe
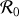 a pour composante
a pour composante
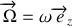 . On peut exprimer ce vecteur dans la base
. On peut exprimer ce vecteur dans la base
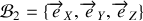 :
:
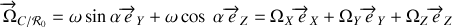
l'axe
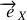 étant choisi perpendiculaire au plan
étant choisi perpendiculaire au plan
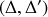 .
.
L'énergie cinétique est alors triviale à calculer :
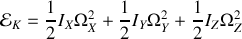
Pour déterminer le tenseur d'inertie dans la base
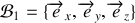 , utilisons l'expression déterminée dans la base
, utilisons l'expression déterminée dans la base
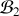 et la matrice de changement de base de
et la matrice de changement de base de
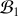 à
à
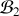 :
:
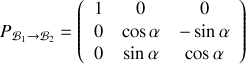
C'est une matrice de rotation d'un angle
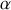 suivant l'axe
suivant l'axe
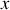 . On peut alors obtenir le tenseur d'inertie
. On peut alors obtenir le tenseur d'inertie
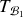 dans la base
dans la base
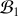 en effectuant le changement de base
en effectuant le changement de base
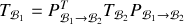
on obtient
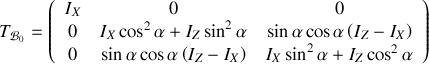
Calculons maintenant le moment cinétique du cylindre au point
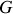 dans la base
dans la base
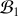 :
:
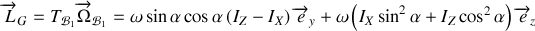
Dans le cas particulier
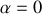 , on retrouve la valeur attendue pour le moment cinétique
, on retrouve la valeur attendue pour le moment cinétique
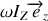 . On remarque que le moment cinétique n'est pas aligné avec l'axe de rotation mais dans le plan
. On remarque que le moment cinétique n'est pas aligné avec l'axe de rotation mais dans le plan
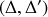 .
.
Appelons
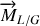 le moment des forces de liaisons du bâti sur l'axe de rotation
le moment des forces de liaisons du bâti sur l'axe de rotation
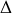 calculé au point
calculé au point
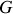 . Le moment du poids calculé au point
. Le moment du poids calculé au point
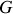 est nul. Il en sort que les moments des forces extérieures agissant sur le cylindre se résume à
est nul. Il en sort que les moments des forces extérieures agissant sur le cylindre se résume à
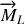 . Nous pouvons maintenant appliquer le théorème du moment cinétique dans le repère galiléen
. Nous pouvons maintenant appliquer le théorème du moment cinétique dans le repère galiléen
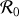
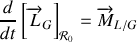
Dans l'expression dont nous disposons pour le moment cinétique, le vecteur
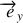 n'est pas fixe par rapport à la base
n'est pas fixe par rapport à la base
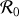 mais effectue une rotation de vitesse angulaire
mais effectue une rotation de vitesse angulaire
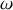 dans le plan
dans le plan
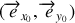 . En choisissant l'origine des temps dans une configuration où les vecteurs
. En choisissant l'origine des temps dans une configuration où les vecteurs
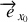 et
et
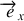 sont confondus on obtient
sont confondus on obtient
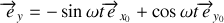
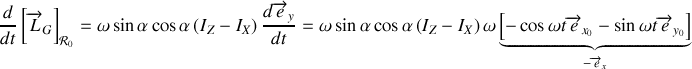
On en déduit le moment des forces de liaison :
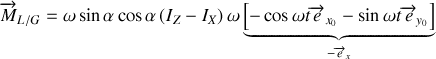
qui est porté par l'axe tournant
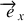 . Bien entendu, le moment des forces de l'axe de rotation sur le bâti est l'opposé. Remarquons que le moment des forces de liaison s'annule si l'axe de rotation est confondu avec un axe principal du solide
. Bien entendu, le moment des forces de l'axe de rotation sur le bâti est l'opposé. Remarquons que le moment des forces de liaison s'annule si l'axe de rotation est confondu avec un axe principal du solide
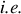
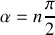 avec
avec
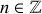 où si l'axe de rotation est dans un plan principal
où si l'axe de rotation est dans un plan principal
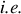
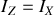 .
.



