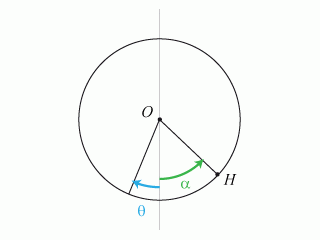
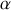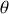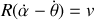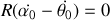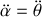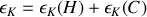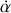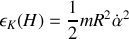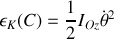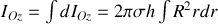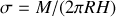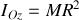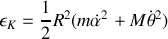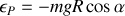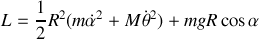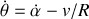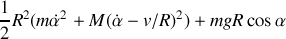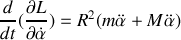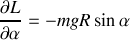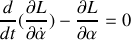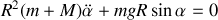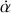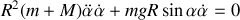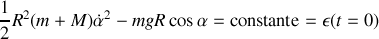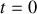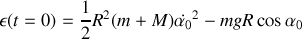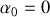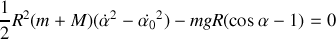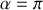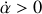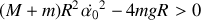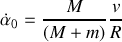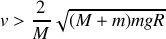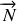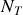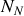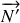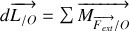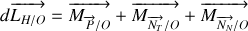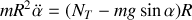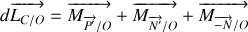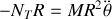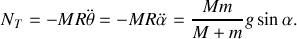Soit l'angle
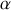 avec la verticale définissant la position du hamster.
avec la verticale définissant la position du hamster.
Soit l'angle
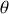 avec la verticale définissant la position de la cage.
avec la verticale définissant la position de la cage.
Le système étant supposé isolé, la vitesse relative est constante :
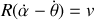 et en particulier à l'instant initial :
et en particulier à l'instant initial :
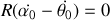 ou encore
ou encore
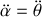
Pour le système total, hamster et cage, écrivons le Lagrangien, ce qui permet de ne pas considérer les forces de liaison.
Un degré de liberté
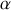 suffit pour décrire le mouvement du système,
suffit pour décrire le mouvement du système,
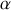 et
et
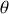 n'étant pas indépendants.
n'étant pas indépendants.
L'énergie cinétique du système total est :
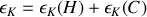
Le hamster effectue un mouvement circulaire de rayon R à la vitesse angulaire
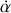 ,
,
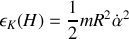
Pour la cage,
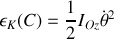
Calculons le moment d'inertie du cylindre, dont la masse n'est répartie qu'en surface, par rapport à l'axe Oz :
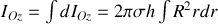
avec
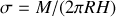
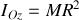
donc
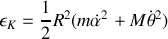
Seul le poids du hamster contribue à l'énergie potentielle, soit :
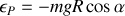 , l'origine étant prise en O.
, l'origine étant prise en O.
Le lagrangien s'écrit donc :
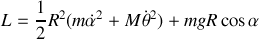
or
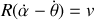
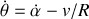
Remplaçons dans le lagrangien :
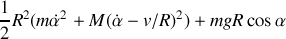
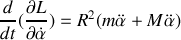
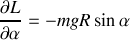
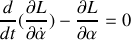
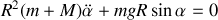
On retrouve l'équation d'un mouvement pendulaire. Le système étant conservatif, retrouvons l'intégrale première caractéristique de la conservation de l'énergie mécanique en multipliant par
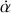 .
.
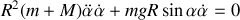
En intégrant,
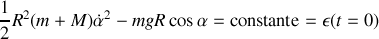
À
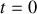 ,
,
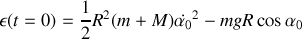 or
or
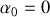
Soit
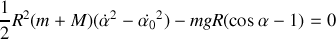
Pour le hamster atteigne le point le plus haut, il faut
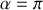 et
et
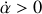
soit
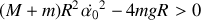
Or on a montré que
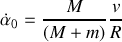
On obtient donc
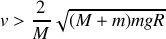
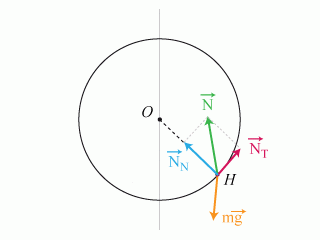
On applique le théorème du moment cinétique à chaque sous-système en introduisant les forces de liaison.
On distinguera la réaction de la cage sur le hamster
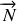 en distinguant la composante tangentielle
en distinguant la composante tangentielle
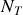 et la composante normale
et la composante normale
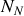
ainsi que la réaction de l'axe sur la cage
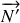
Écrivons le théorème du moment cinétique en O :
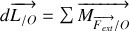
Pour le hamster,
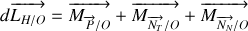
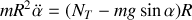
Pour la cage,
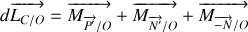
où il ne reste que
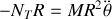
Avec ces 2 équations, on retrouve l'équation différentielle trouvée en 1) avec en plus,
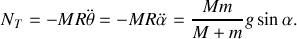
On établira la vitesse minimale comme précédemment.
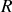 pouvant tourner autour de son axe propre
pouvant tourner autour de son axe propre
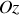 fixe, héberge un hamster
fixe, héberge un hamster
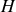 . La cage a une masse
. La cage a une masse
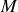 supposée régulièrement répartie sur la périphérie. Le hamster supposé ponctuel de masse
supposée régulièrement répartie sur la périphérie. Le hamster supposé ponctuel de masse
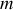 , initialement au repos au point le plus bas, part brusquement avec une vitesse
, initialement au repos au point le plus bas, part brusquement avec une vitesse
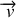 par rapport à la cage. Le système 'hamster+cage' est isolé avant le départ du hamster puis juste après.
par rapport à la cage. Le système 'hamster+cage' est isolé avant le départ du hamster puis juste après.