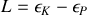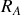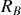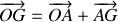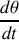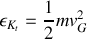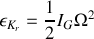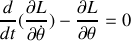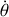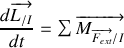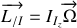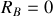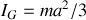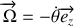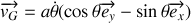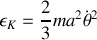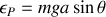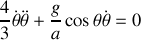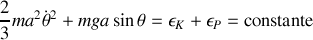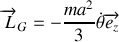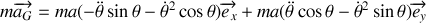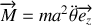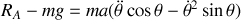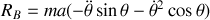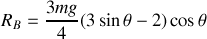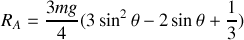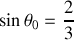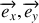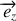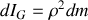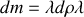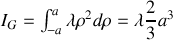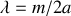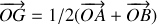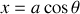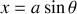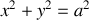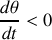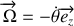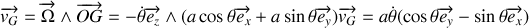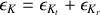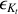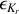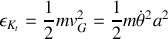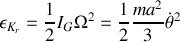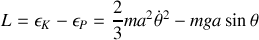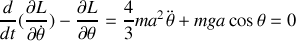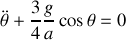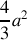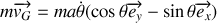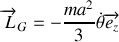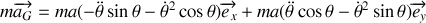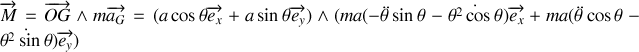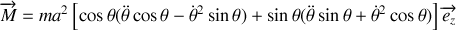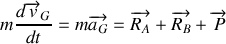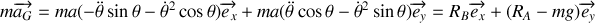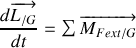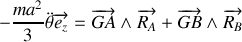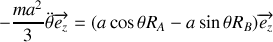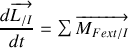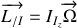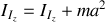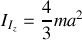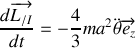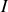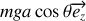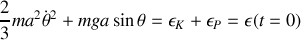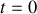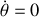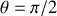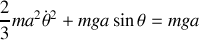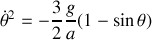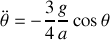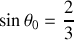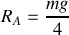Énoncé
Une échelle AB de masse
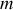, de longueur
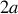est assimilée à une barre homogène d'épaisseur négligeable.
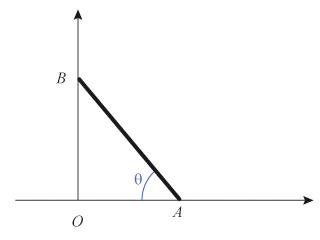
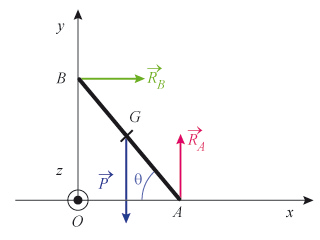
Quelle condition de contact doit être vérifiée pour que l'échelle tienne en équilibre ? Elle est en contact sans frottement sur le sol horizontal en A et sur le mur vertical en B. On note
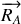et
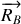les réactions du sol et du mur sur l'échelle. Elle est lâchée sans vitesse initiale pour
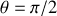.Calculez son moment d'inertie
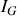autour d'un axe perpendiculaire à AB passant par son centre de masse G.Quelle est la trajectoire du centre de masse G?
Quel est le nombre de degrés de liberté ? Quelle variable décrit le mouvement de la tige ? Définir le vecteur rotation associé au mouvement de la barre.
Le torseur cinématique est défini par le couple de vecteurs (
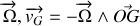). Exprimer chacune de ces composantes vectorielles en fonction de
,
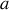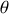et de leurs dérivées.Quelle est l'énergie cinétique totale de la barre?
Quelle est son énergie potentielle?
Donner le lagrangien ainsi que l'équation du mouvement. Retrouver la conservation de l'énergie mécanique totale.
Le torseur cinétique est défini par (
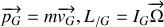) et le torseur dynamique par (
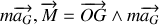). Exprimer chacune de ces composantes vectorielles en fonction de
,
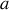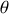, de leurs dérivées.Appliquer les théorèmes du centre d'inertie et du moment cinétique en G. En déduire l'équation différentielle vérifiée par
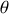.Appliquer le théorème du moment cinétique au point I formant un rectangle avec O, A et B. Retrouver l'équation différentielle vérifiée par
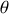.Déterminer les réactions en A et B en fonction de
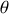.Montrer que le contact en B cesse pour une valeur
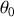de
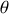. Calculer la réaction en A pour cette valeur.
