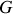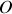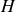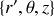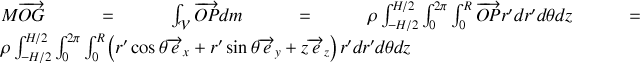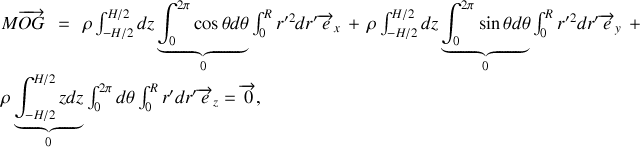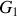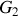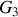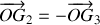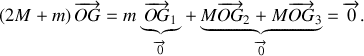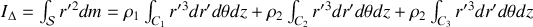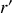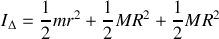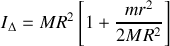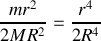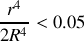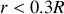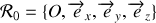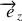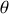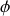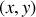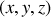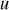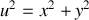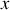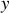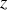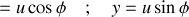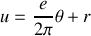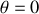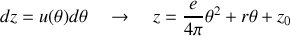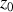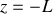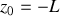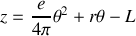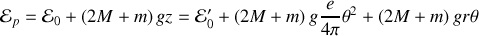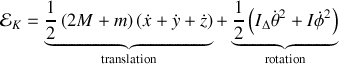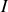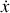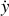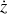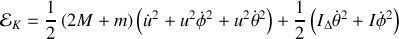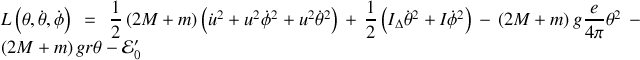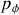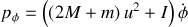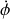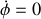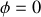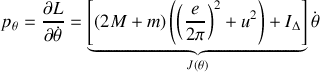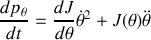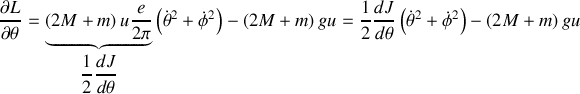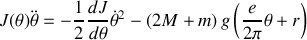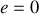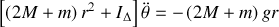Montrons au préalable le centre de gravité
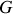 d'un cylindre homogène de masse
d'un cylindre homogène de masse
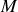 , de centre
, de centre
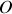 , de rayon
, de rayon
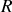 et de hauteur
et de hauteur
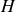 est confondu avec
est confondu avec
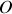 . Le calcul est simple dans une base cylindrique
. Le calcul est simple dans une base cylindrique
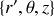 .
.
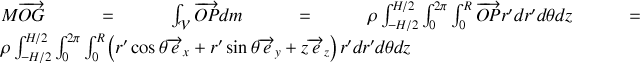
Soit en séparant les intégrales :
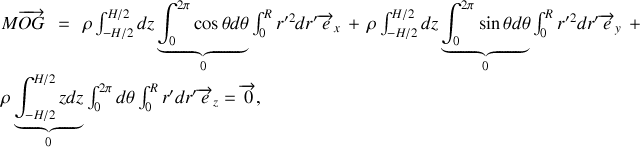
ce qui démontre bien le résultat.
On peut maintenant calculer le centre de gravité
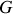 de
de
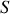 en le décomposant en trois cylindres homogènes. En appelant
en le décomposant en trois cylindres homogènes. En appelant
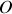 le centre du solide
le centre du solide
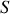 , le centre de gravité
, le centre de gravité
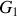 de
de
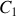 est en
est en
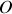 , les centres de gravité
, les centres de gravité
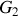 et
et
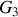 sont tels que
sont tels que
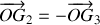 dès lors il vient
dès lors il vient
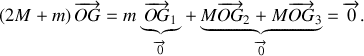
Le centre de gravité
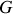 est évidement confondu avec
est évidement confondu avec
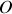 .
.
Passons au calcul du moment d'inertie :
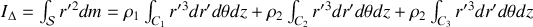
où
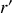 est la distance du point courant à l'axe
est la distance du point courant à l'axe
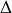 , après calcul de chaque intégrale on obtient
, après calcul de chaque intégrale on obtient
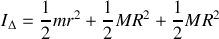
soit encore
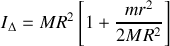 .
.
On introduit un repère cartésien
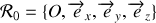 avec l'axe
avec l'axe
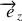 dirigé suivant la verticale ascendante. En l'absence de contrainte géométrique le solide
dirigé suivant la verticale ascendante. En l'absence de contrainte géométrique le solide
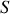 à trois degrés de liberté de translation et trois degrés de liberté de rotation. Comme l'axe
à trois degrés de liberté de translation et trois degrés de liberté de rotation. Comme l'axe
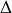 est horizontal, il n'y a que deux degrés de rotation et comme la corde dévidée est verticale, les trois degrés de liberté de translation sont liés directement aux deux rotations. Finalement, le yo-yo possède donc deux degrés de liberté.
est horizontal, il n'y a que deux degrés de rotation et comme la corde dévidée est verticale, les trois degrés de liberté de translation sont liés directement aux deux rotations. Finalement, le yo-yo possède donc deux degrés de liberté.
On note
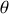 l'angle de rotation du yo-yo autour de l'axe
l'angle de rotation du yo-yo autour de l'axe
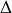 et
et
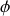 l'angle de rotation de
l'angle de rotation de
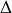 dans le plan
dans le plan
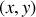 . On appelle
. On appelle
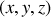 les coordonnées cartésiennes du point
les coordonnées cartésiennes du point
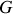 . On introduit aussi la distance
. On introduit aussi la distance
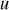 du centre de gravité
du centre de gravité
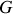 à l'axe
à l'axe
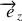 , il est évident que
, il est évident que
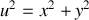 .
.
Il faut maintenant réaliser le lien entre les deux variables angulaires
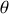 et
et
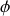 et les variables de translation
et les variables de translation
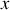 ,
,
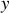 et
et
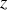 . Les coordonnées dans le plan horizontal sont liées à la rotation d'angle
. Les coordonnées dans le plan horizontal sont liées à la rotation d'angle
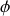 et à la distance
et à la distance
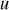 : x
: x
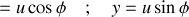
La distance
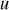 est liée à l'angle de rotation
est liée à l'angle de rotation
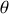 puisque la corde s'enroule en spirale
puisque la corde s'enroule en spirale
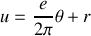
où l'on a pris comme référence
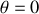 lorsque toute la corde est dévidée. Enfin, l'altitude
lorsque toute la corde est dévidée. Enfin, l'altitude
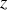 est aussi reliée à l'angle
est aussi reliée à l'angle
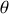 du fait du dévidement de la corde :
du fait du dévidement de la corde :
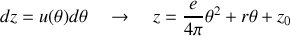
la constante
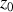 se détermine quand
se détermine quand
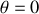 alors
alors
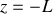 soit
soit
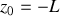 et finalement
et finalement
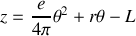 .
.
Déterminons l'énergie potentielle :
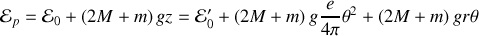
On peut maintenant déterminer l'énergie cinétique
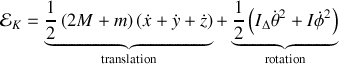
où l'on a introduit
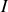 le moment de rotation de
le moment de rotation de
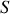 une direction transverse à
une direction transverse à
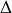 . En remplaçant les variables
. En remplaçant les variables
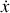 ,
,
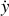 et
et
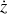 par leurs expressions en fonction de
par leurs expressions en fonction de
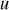
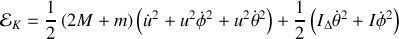
Le Lagrangien vaut
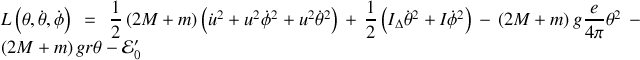
Avant d'aller plus loin en remplaçant
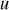 , on peut noter que
, on peut noter que
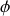 est une coordonnée cyclique est que donc l'impulsion
est une coordonnée cyclique est que donc l'impulsion
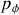 est une constante du mouvement
est une constante du mouvement
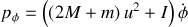
ce qui implique que
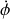 est une constante du mouvement. On se placera dans le cas où
est une constante du mouvement. On se placera dans le cas où
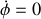 et on choisira
et on choisira
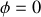 .
.
Écrivons maintenant l'équation pour la variable
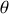 , calculons en premier lieu l'accélération généralisée
, calculons en premier lieu l'accélération généralisée
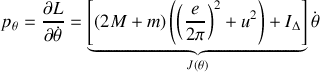
et donc
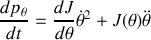 ;
;
puis la force généralisée
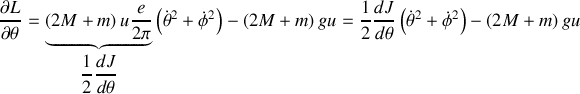
Soit finalement en posant
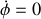
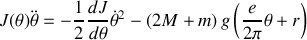
Si
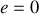 , l'équation du mouvement devient
, l'équation du mouvement devient
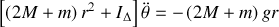
ce qui correspond à un mouvement uniformément accéléré.
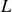 de diamètre
de diamètre
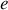 et de masse négligeable s'enroulant en spirale sur un cylindre
et de masse négligeable s'enroulant en spirale sur un cylindre
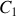 de masse
de masse
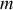 , de rayon
, de rayon
 et de longueur
et de longueur
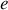 . Le cylindre
. Le cylindre
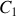 est bordé de deux cylindres identiques
est bordé de deux cylindres identiques
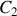 et
et
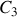 de masse
de masse
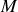 et de rayon
et de rayon
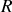 . Les trois cylindres
. Les trois cylindres
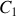 ,
,
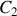 et
et
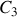 sont homogènes et coaxiaux d'axe
sont homogènes et coaxiaux d'axe
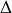 ; ils forment le solide noté
; ils forment le solide noté
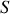 .
.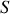 et son moment d'inertie
et son moment d'inertie
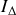 par rapport à l'axe
par rapport à l'axe
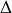 .
.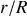 peut-on négliger la contribution du cylindre central
peut-on négliger la contribution du cylindre central
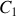 à l'inertie du solide
à l'inertie du solide
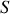 si les trois cylindres ont la même densité et la même longueur?
si les trois cylindres ont la même densité et la même longueur? 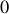 fixe par rapport à un référentiel Galiléen. Donner le nombre de degrés de liberté du système en supposant que la corde dévidée reste toujours verticale et que l'axe
fixe par rapport à un référentiel Galiléen. Donner le nombre de degrés de liberté du système en supposant que la corde dévidée reste toujours verticale et que l'axe
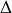 reste horizontal. Déterminer l'équation du mouvement du yo-yo. Donner la solution dans le cas d'une corde d'épaisseur nulle.
reste horizontal. Déterminer l'équation du mouvement du yo-yo. Donner la solution dans le cas d'une corde d'épaisseur nulle.