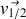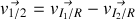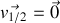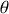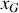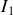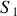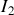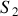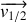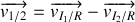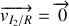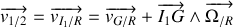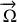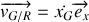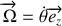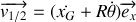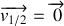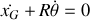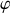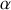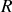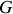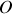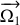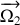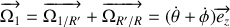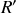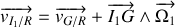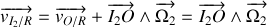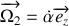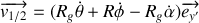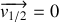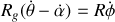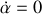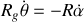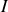Considérons la variable
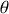 , représentant l'angle de rotation d'un point du disque avec l'axe vertical et
, représentant l'angle de rotation d'un point du disque avec l'axe vertical et
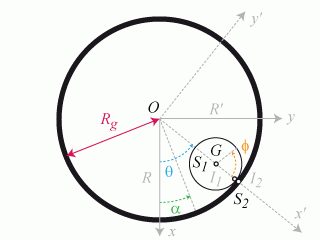
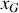 la coordonnée du centre d'inertie. Soient I le point géométrique de contact des 2 solides
la coordonnée du centre d'inertie. Soient I le point géométrique de contact des 2 solides
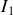 le point du disque (
le point du disque (
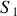 ) qui coïncide avec I à l'instant considéré et
) qui coïncide avec I à l'instant considéré et
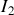 le point du plan (
le point du plan (
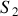 ) qui coïncide avec I au même instant.
) qui coïncide avec I au même instant.
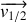 désigne la vitesse de glissement du disque sur le plan.
désigne la vitesse de glissement du disque sur le plan.
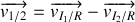
Le plan est immobile :
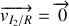
Les points
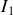 et G appartiennent au même solide :
et G appartiennent au même solide :
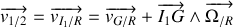
avec
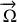 le vecteur rotation du disque.
le vecteur rotation du disque.
Or
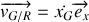 et
et
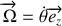
donc la vitesse de glissement s'écrit :
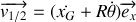
Dans le cas d'un roulement sans glissement,
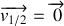 et
et
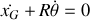
Soient
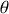 et
et
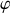 définissant la position d'un point du disque
définissant la position d'un point du disque
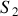 .
.
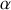 repère la position du guide
repère la position du guide
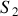 par rapport au référentiel
par rapport au référentiel
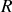 . De même qu'en 1.,
. De même qu'en 1.,
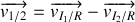
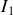 et
et
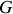 appartiennent au disque
appartiennent au disque
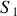
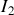 et
et
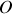 appartiennent au guide
appartiennent au guide
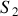
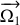 et
et
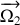 désignent les vecteurs rotation de chacun des solides dans le référentiel
désignent les vecteurs rotation de chacun des solides dans le référentiel
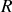
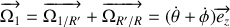
avec
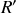 le référentiel lié au disque
le référentiel lié au disque
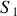
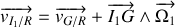
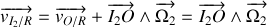
avec
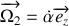
Dans la base de
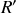 , la vitesse de glissement s'écrit donc :
, la vitesse de glissement s'écrit donc :
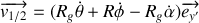
S'il n'y a pas glissement,
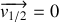 donc
donc
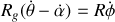
Si le guide est fixe dans
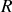 ,
,
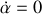 ,
,
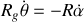 , ce qui revient à écrire l'égalité des longueurs parcourues par le point géométrique
, ce qui revient à écrire l'égalité des longueurs parcourues par le point géométrique
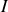 sur le disque et sur le guide.
sur le disque et sur le guide.
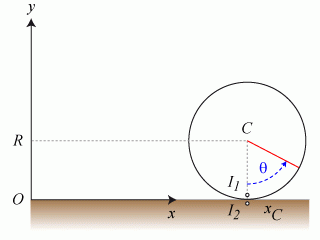
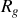 en mouvement. Exprimer la vitesse de glissement du disque sur le guide. Écrire la condition de roulement sans glissement.
en mouvement. Exprimer la vitesse de glissement du disque sur le guide. Écrire la condition de roulement sans glissement.