Formalisme vectoriel de Newton : théorème du centre d'inertie
Dans le formalisme vectoriel, le principe fondamental de la dynamique pour chaque point matériel
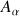permet de déduire la variation d'impulsion au cours du temps
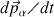produite par la résultante
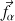des forces qui s'appliquent sur le point
.
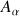Pour un solide, le PFD reste valide pour chaque élément composant le solide.
La somme de toutes les variations de quantités de mouvement peut être effectuée selon :
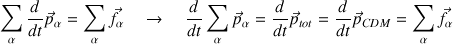
Ainsi apparaît naturellement le théorème du centre d'inertie, équivalent du PFD mais appliqué au point particulier qu'est le centre d'inertie :
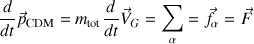
valide si la masse du système est invariante.
La résultante des forces appliquées tient compte, en principe, de toutes les forces ; mais les forces internes au solide, qui s'annulent deux à deux en vertu du principe d'action et de réaction, disparaissent de sorte que ne subsistent que les forces externes.
Remarque :
Cette relation vectorielle concerne les 3 directions de l'espace et n'implique pas les points d'application des forces, considérées alors comme des vecteurs glissants : seules les directions importent.
Ce ne sera pas le cas des moments de forces et de l'évaluation de l'énergie potentielle du solide.
En prévision de la formulation lagrangienne du mouvement global mais également des mouvements de rotation du solide, une propriété particulière du champ de force homogène est pointée ci-après.
