Formulation lagrangienne du mouvement global
L'uniformité du formalisme lagrangien permet d'écrire les équations du mouvement directement à partir du lagrangien du solide lequel est construit à partir de ses énergies cinétique et potentielle.
Le mouvement de translation est décrit par le mouvement du CDM repéré par son rayon vecteur
.
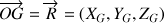Les coordonnées sont notées également
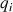où
.
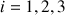La masse totale du solide est
.
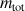L'énergie cinétique de translation est
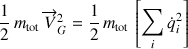. L'énergie cinétique de rotation est décrite par d'autres variables, angulaires.
L'énergie potentielle du solide dépend des coordonnées de chaque point matériel :
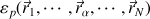
et, à titre de rappel, sa différentielle vaut :
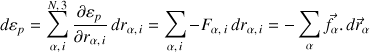
Pour un solide indéformable, les rotations ne sont pas prises en compte et la translation de chaque point matériel est celle du CDM
.
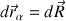La variation d'énergie potentielle s'écrit :
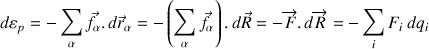
Ainsi le travail élémentaire effectué sur la translation par la résultante des forces est évalué sur le déplacement élémentaire du CDM : la résultante
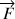est appliquée au CDM.
La fonction de Lagrange décrivant la translation s'écrit :
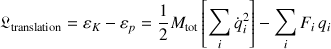
De sorte que les équations du mouvement relatives à la translation du CDM dérivées du formalisme lagrangien sont :
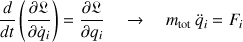
Elles correspondent aux
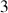composantes du théorème du centre d'inertie.
Le mouvement de translation du CDM est ici décrit par sa propre énergie cinétique.
La variation de sa quantité de mouvement (un vecteur), ou impulsions généralisées, est produite par des forces généralisées, toutes déduites de l'énergie potentielle totale.
