Champ de force homogène : énergie potentielle du solide
Le champ de force homogène, ou uniforme, est caractéristique des forces agissant selon une direction fixe : pesanteur, champ électrique uniforme...
Ainsi chaque particule du solide est soumise à son poids toujours dirigé selon le champ de pesanteur
.
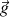La question qui se pose porte sur le point d'application de la résultante de ces forces sachant que sa direction et son sens sont définis vectoriellement.
Pour répondre à cette question, il faut noter que la grandeur qui fait appel au point d'application est la grandeur moment angulaire (cinétique).
Dans le cas du champ de forces homogène, il existe un ensemble de points, définissant une direction, par rapport à laquelle le moment de cette force est toujours nul. Cette condition est par ailleurs nécessaire pour décrire l'équilibre d'un solide sous l'action du champ de forces.
Ce qui suit montre que cette direction est celle du champ et qu'elle passe par un point particulier qui devient de plus en plus familier.
Démonstration :
Par définition, la force, qui est appliquée en
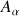, et son moment sont toujours perpendiculaires et cela, quelle que soit l'origine du calcul
.
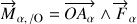S'il existe une origine
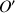telle que le moment de la force soit nul :
,
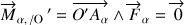alors l'écriture du moment de la force devient indépendant de son point d'application selon :
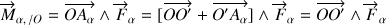
Cette propriété du point
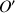, s'il existe, est de fait partagée par tous les points d'un axe passant par
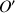et parallèle à
.
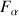En effet, tout point
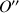défini par
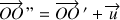
et tel que
,
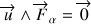preuve que la direction
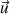est parallèle à celle de la force
,
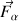ce point
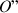vérifie la condition
.
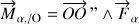Dans le cas d'un champ de forces, cette direction est unique : c'est celle de la résultante des forces.
Et le point
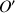est partagé par toutes les forces.
Si l'origine
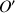existe alors tout champ de forces homogène possède un point où le moment des forces est nul.
Le passage au moment total est alors évident puisque :
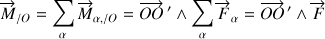
La résultante des forces apparaît ainsi que son point d'application
.
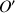En toute généralité, cette démonstration décrit une ligne qui représente la direction du champ, mais un seul point présente un intérêt, le point
.
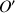Il peut être visualisé sur l'exemple suivant.
Exemple : Cas du champ de pesanteur
Dans le cas du champ de pesanteur, homogène selon
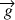, la direction
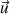est évidente.
La résultante des forces est :
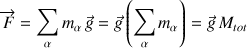
Le moment total par rapport à un point
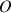quelconque est :
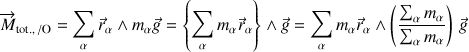
ou encore :
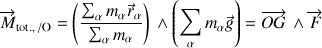
Le centre de masse, et centre d'inertie, est le point d'application de la résultante des forces de pesanteur et de tout champ de forces uniforme, quel que soit son expression.
Et une propriété supplémentaire est à mettre à son actif : le moment résultant du champ de forces y est nul. C'est un centre d'inertie en rotation également.
Il permet de réaliser un équilibre en rotation.
L'importance du point d'application de la résultante des forces sera confortée par ce qui va suivre où l'énergie potentielle est rapportée à un champ d'espace dès l'étude du mouvement global de translation.
