Conditions d'équilibre d'un solide.
Partant des équations du mouvement obtenues soit par le formalisme lagrangien soit par les théorèmes généraux, l'absence de mouvement s'exprime par des dérivées temporelles nulles : l'extension du principe d'inertie au solide est alors obtenue.
Définition :
L'équilibre d'un système solide a lieu lorsque les résultantes des forces et de leurs moments sont nulles.
Il est décrit par le couple d'équations :
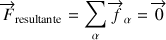
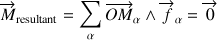
Ainsi pour un système de corps solides en contact les uns avec les autres, l'équilibre a lieu lorsque ces conditions sont satisfaites pour chaque corps séparément, en incluant les forces de réaction aux points de contact appliquées au corps étudié (isolé).
Mais dans la pratique, l'équilibre est obtenu pour un agencement des forces (des contraintes) donné. Certaines forces sont connues , d'autres sont à déterminer.
Méthode :
Concrètement, les équations décrivant les conditions d'équilibre sont vectorielles et il faudra autant d'équations que d'inconnues : souvent les forces de contact.
Ces conditions d'équilibre seront donc répétées judicieusement sur les différents constituants du système pour déterminer les inconnues manquantes.
Le point de départ est, le plus souvent, l'équilibre du système dans sa globalité avec ses forces extérieures et les réactions aux points de contact avec le milieu extérieur. Dans ce cas, les forces internes se neutralisent et n'apparaissent pas. Si le nombre d'inconnues est plus élevé que le nombre d'équations, le passage par l'isolement d'un ou de plusieurs éléments du système est nécessaire ; mais la contrepartie est l'apparition de forces internes sous forme de réaction du support du sous système.





