Exemple de contrainte de contact
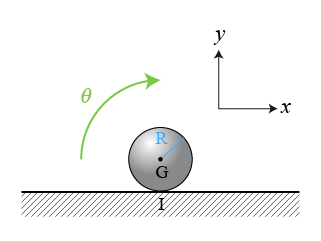
Le roulement pur d'une sphère sur une surface plane est un exemple simple de liaison.
Si
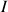est le point de contact sphère par rapport au sol et
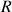son rayon (Fig.11), le mouvement du centre de la sphère
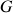définit la translation d'ensemble.
La vitesse du point de contact est toujours :
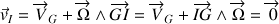
pour le roulement pur.
L'équation de la contrainte (roulement sans glissement) pour les vitesses est alors
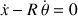, la vitesse du point de contact
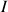ou
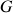étant horizontale.
Le vecteur vitesse angulaire est toujours perpendiculaire au plan de la figure et rentrant pour une rotation dans le sens opposé à la trigonométrie.
Plan incliné ou horizontal, la contrainte s'exprime à l'identique. Les axes seuls ont été adaptés.
L'équation de liaison est intégrable pour donner :
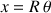, associant ainsi les deux variables potentielles du problème.
C'est une contrainte holonome.
