Équations de Lagrange et liaisons
En cas de liaisons non holonomes ou holonomes complexes, toutes les coordonnées (
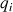), dont celles non indépendantes (
,
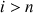nombre de degrés de liberté), doivent être utilisées.
En effet certaines coordonnées ne sont pas indépendantes. Des liaisons existent et sont représentées par les équations holonomes suivantes pour chaque contrainte
:
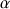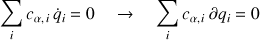
où les variations portent sur les coordonnées généralisées
Un nouveau lagrangien est construit : les équations des liaisons sont ajoutées à la description, multipliées par des multiplicateurs de Lagrange associés. (Voir grain 2)
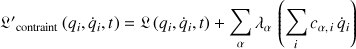
Pour des contraintes holonomes, le principe de moindre action est modifié selon :
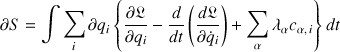
La présence de liaisons modifie également les équations de Lagrange selon :
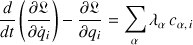
Ces équations définissent autant d'équations du mouvement que de variables (inconnues), comprenant en plus
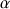multiplicateurs de Lagrange qui sont également inconnus.
Pour résoudre le problème, il faudra ajouter aux équations de Lagrange autant d'équations de contraintes que de multiplicateurs de Lagrange utilisés, soit
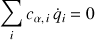permettant ainsi d'avoir autant d'équations que d'inconnues.
Mais où sont donc les forces de contact dans ce formalisme ?
Elles sont obtenues dans la signification des multiplicateurs de Lagrange comme dans l'exemple ci-après.
Exemple : Mouvement du balancier d'une horloge
Le mouvement pendulaire du CDM d'un pendule pesant, de forme géométrique quelconque, de masse
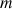, situé à la longueur
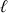de l'axe de rotation, est analysé en coordonnées cartésiennes
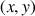avec le formalisme lagrangien.
L'équation de la contrainte peut être ajoutée sous la forme
.
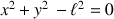Les coordonnées
et
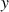repèrent donc le CDM.
L'énergie cinétique est :
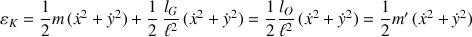
grandeur qui regroupe les énergies cinétiques de translation du CDM et de rotation de l'ensemble (le théorème de Huygens a été appliqué :
).
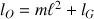L'énergie potentielle du CDM s'écrit simplement :
.
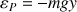Avec la relation
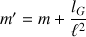, le solide ‘horloge' possède une inertie plus grande que celle d'un pendule simple.
L'axe
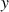est dirigé vers le bas
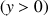et l'origine des énergies potentielles (
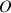) est située au point d'accroche du pendule et des axes.
Si la contrainte n'est pas prise en compte, les équations du mouvement obtenues sont celles d'une chute libre.
Les coordonnées
et
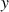ne sont pas les coordonnées adaptées au système, ses coordonnées généralisées puisqu'une contraintes les lie.
Le lagrangien contraint est :
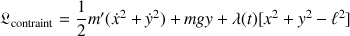
Les deux équations d'Euler-Lagrange s'écrivent :
Auxquelles s'ajoute l'équation de la contrainte.
Le multiplicateur de Lagrange apparaît comme une force par unité de longueur, projetée ici sur les deux axes.
L'équation de contrainte, dérivée deux fois par rapport au temps, permet de déduire deux propriétés :
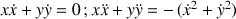
La seconde relation apparaît en manipulant les équations de Lagrange sous la forme :
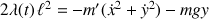
Cette équation est plus expressive en notations polaires. Elle sera développée plus loin.
L'utilisation de la conservation de l'énergie mécanique totale permet d'écrire cette relation sous une forme associant uniquement les inconnues
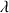et
:
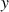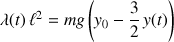
Pour un lâcher de l'horloge d'une hauteur
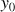sans vitesse initiale.
L'équation différentielle vérifiée par la variable
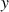est :
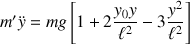
Lorsque l'ordonnée du CDM
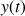est obtenue : en multipliant par
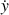l'équation ci-dessus, la forme polynomiale de
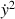, fonction de
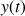, apparaît, elle est reportée dans
.
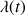L'expression obtenue est alors injectée dans l'équation différentielle vérifiée par
.
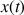Mathématiquement lourd mais instructif.
En coordonnées polaires :
Si
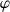est l'angle avec l'horizontale et
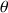celui avec la verticale, le passage en coordonnées polaires, (
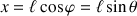et
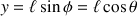), est plus visuel et permet de retrouver les projections du second principe de Newton sur les directions
et
:
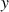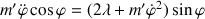
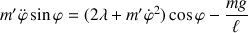
En multipliant la première par
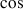et la seconde par
et après une somme des deux équations, l'équation angulaire de l'oscillation apparaît, équivalent au théorème du moment cinétique appliqué en
:
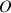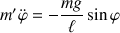
et où l'effet de la contrainte (via
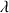) n'apparaît pas.
La force de contact est radiale.
Ainsi en multipliant la première par
et la seconde par
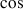et après une soustraction, l'équation suivante apparaît :
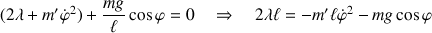
La force du membre de gauche équilibre les deux (centrifuge et composante du poids) du membre de droite.
Cette relation est identique à son équivalente cartésienne si l'équivalence
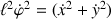est notée.
La signification de la contrainte aux équations peut être ainsi directement associée à "une tension de fil" (comme pour un pendule simple) qui n'apparaît que sur l'axe radial
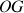et qui s'applique au point de contact
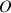. (le lagrangien non contraint décrit la chute libre du CDM)
Le passage au pendule pesant dans cet exercice est simple.
Les variables
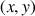caractérisant la position du CDM, avec sa translation, l'effet massif du solide apparaît avec une rotation d'ensemble autour du point d'accrochage du balancier.
Le moment d'inertie est alors considéré par rapport à un axe passant par ce point et perpendiculaire au plan du mouvement
.
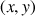L'expression de la vitesse angulaire (
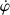ou
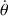) est donnée par les coordonnées polaires ci-dessus en fonction de
et
.
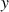Un autre exercice d'application figure dans le cours sur le formalisme lagrangien.
Il concerne le roulement pur d'une sphère sur un plan incliné.
