Équilibre de l'échelle double
Deux échelles, de longueur
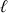, sont adossées l'une à l'autre par leur sommet
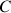et, pour des raisons d'équilibre devenues évidentes, sont retenues par une corde à leur base.
Le poids de la tige (échelles différentes ou objet sur l'échelle
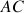ou autre), noté
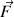est porté par le milieu de la tige
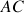. Ceci produit une dissymétrie de l'action du poids aux points de contact
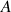et
.
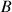La prise en compte des deux éléments de la double échelle produit la relation suivante :
.
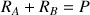Pour déterminer plus d'éléments il est nécessaire de dissocier une partie de l'échelle, par exemple celle
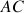, et lui appliquer les deux conditions d'équilibre.
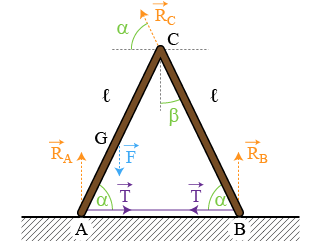
Lorsque la partie
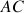est isolée, elle subit l'effet des forces
,
,
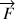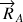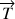et
.
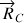L'application des conditions d'équilibre produit les
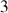équations suivantes :
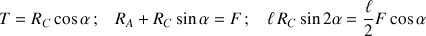
Le moment résultant a été évalué en
.
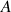et la solution obtenue est :
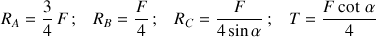
Une extension possible de cet exercice est de considérer une force
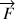, appliquée en un point quelconque
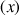de la barre, pour déterminer par exemple les conditions d'équilibre en fonction de
et trouver un équilibre stable, s'il existe.
