Roulement d'une sphère homogène sur un plan
Le roulement s'effectue sans glissement sous l'action d'une force
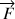et d'un moment de force
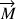extérieurs.
Lorsque la détermination des forces de contact est un objectif, l'utilisation des théorèmes généraux et du formalisme vectoriel est une voie obligée.
La sphère, de rayon
, est soumise, en plus de la force extérieure
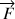et du moment extérieur
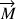(qui peut être un frottement de roulement par exemple), à une force de contact
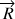(réaction du support ou force de liaison) ainsi qu'à son moment (de la force de liaison ou de contact).
L'ensemble de ces forces possèdent
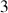composantes, dans le cas général et sans données complémentaires.
Elles interviennent dans les théorèmes du centre d'inertie :
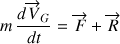
mais également dans celui du moment cinétique appliqué au CDM :
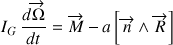
Le moment de la force de réaction
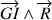est exprimé au moyen de la normale
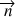au point de contact
.
La condition de roulement sans glissement est obtenue en annulant la vitesse instantanée au point de contact.
Ainsi
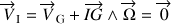
produit la condition
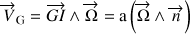
qui est dérivée par rapport au temps pour déduire la relation suivante :
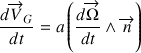
Cette relation exprime un mouvement dans le plan perpendiculaire à la normale et donc un contact.
Cette propriété est à l'origine d'une relation vectorielle couplant forces et moments obtenue en remplaçant la dérivée de la vitesse angulaire (théorème du moment cinétique) :
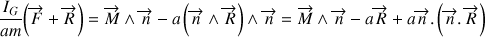
Cette relation permet de déduire les trois composantes de la réaction en fonction des forces et moments à l'origine du mouvement.
Reportées dans les équations du formalisme vectoriel (théorème du centre d'inertie et du moment cinétique), elles permettent de déduire les variations temporelles des vitesses du CDM et angulaire, directement accessibles par le formalisme lagrangien.
Dans le cas général, la force extérieure a trois composantes :
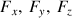et la force inconnue est la réaction au point de contact, également trois composantes
.
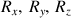La relation produit trois équations pour trois inconnues dont les solutions pour la sphère sont :
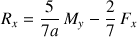
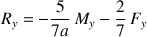
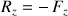
La dernière équation marque le contact avec une action de type "poids" et sa réaction.
Les deux autres équations donne toute la richesse du mouvement sur le plan en fonction des forces et moment extérieurs directement associés.
Les accélérations du CDM de la sphère sont alors :
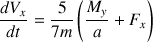
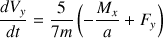
Chaque composante de la force extérieure contribue directement à la composante de l'accélération de translation de la sphère.
Le produit vectoriel fait intervenir les composantes croisées du moment extérieur.
L'accélération angulaire est donnée par :
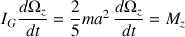
Cette résolution inclut une généralité sur les force et moment extérieurs mais considère une forme sphérique à l'origine d'une égalité entre les
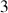moments d'inertie.
Ainsi une géométrie plus complexe, induisant trois moments d'inertie
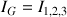selon trois directions de l'espace, par exemple, peut être développée.
La position du centre de masse, par rapport au point de contact, doit alors être adaptée.
