Équations d'Euler dans un référentiel d'axes fixes, lié au solide
Les rotations (
,
,
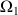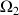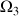) sont exprimées dans le référentiel mobile des axes principaux (
).
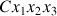Le mouvement dans un référentiel dont les axes sont fixes (
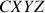) doit prendre en compte l'entraînement dû aux rotations.
Méthode : Application à l'impulsion du solide
A la base de la méthode, la composition des vitesses suivante vérifiée par tout vecteur, noté
:
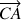Le référentiel mobile tourne autour de celui aux axes fixes : l'entraînement subi est donc une rotation et la vitesse d'entraînement s'écrit :
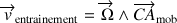
Cette composition des ‘vitesses', qui vaut pour tout vecteur
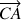, peut être appliquée aux vecteurs IMPULSION (mouvement du centre d'inertie ou CDM, distinct de
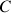) et MOMENT CINÉTIQUE du solide.
Elle permet de décrire toutes variations des grandeurs vitesses, angulaire et linéaire (du CDM), dans l'espace mobile mais d'axes fixes.
L'équation pour le vecteur ‘impulsion' du solide (
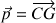) s'écrit généralement selon :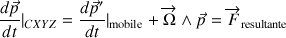
Cette équation exprime également le théorème du centre d'inertie, dans le référentiel initial
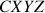, si le point
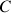est distinct du point
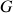, et tient compte de l'entraînement de rotation. La résultante des forces est la signature d'un mouvement global du centre d'inertie.
Le moment cinétique, quant à lui, isole et décrit uniquement les rotations,
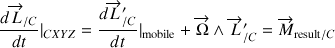
en associant sa variation au moment résultant dans un théorème du moment cinétique.
Tous les membres de droite sont exprimés dans le référentiel mobile, selon les axes propres du solide.
Dans le référentiel initial
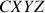l'impulsion du solide de masse
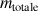vérifie les équations :
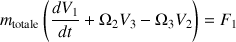
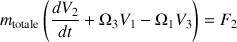
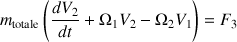
Ici, les trois composantes de l'impulsion,
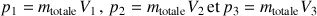sont exprimées dans le référentiel mobile
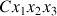, mais elles sont affectées par la rotation.
L'origine de la variation de l'impulsion est la résultante des forces appliquées. Les forces d'inertie de rotation sont également bien identifiées.
Dans un référentiel fixe, celui du laboratoire par exemple, la translation globale du centre
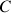apparaîtra sous forme d'une contribution additive qui s'exprimera dans le référentiel fixe. (voir les référentiels non galiléens dans le cours sur les "les bases de la Mécanique Physique")
Ces équations sont paramétrées par la rotation du solide laquelle est décrite par le théorème du moment cinétique qui suit.
Fondamental : Équations d'Euler pour le moment cinétique.
Exprimé dans le référentiel mobile
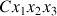, le moment cinétique est déterminé par ses
composantes
.
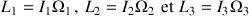Il vérifie les équations D'EULER suivantes :
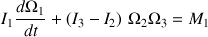
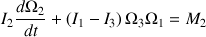
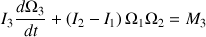
Elles associent l'évolution des vitesses angulaires aux moments des forces qui les produisent.
Ces équations s'appliquent directement à l'application décrite au fil du cours : la rotation libre.
