Application à la rotation libre d'une toupie
La rotation libre est caractérisée par un moment de forces résultant nul.
Les équations d'Euler pour les vitesses angulaires s'écrivent :
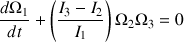
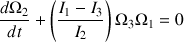
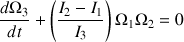
Ce système peut être simplifié car la toupie est symétrique.
Appliquées à la toupie symétrique pour laquelle
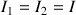les équations d'Euler produisent les
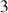équations suivantes :
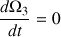. Cette rotation uniforme autour de l'axe
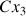permet de définir une vitesse angulaire normalisée
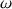selon : 
.Les deux autres équations sont linéaires et couplées :
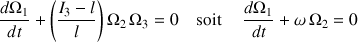
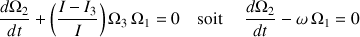
Ces deux dernières équations sont combinées pour obtenir les équations harmoniques, et identiques, suivantes :
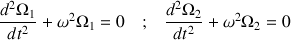
et dont les solutions oscillent à la même pulsation.
Elles sont différentiables à l'amplitude et à la phase, paramètres des solutions. Le résultat final sera en général une composition elliptique.
Le couple de solutions oscillantes pour ce système est par exemple et pour le plus simple :
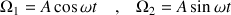
Les conditions initiales ont été choisies telles que la phase relative a été fixée pour réaliser la relation :
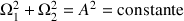
Le vecteur «rotation totale» ainsi obtenu a un module constant puisque
sa projection dans le plan
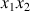est une constante, ainsi que sa projection sur l'axe
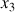de la toupie.
Il tourne autour de l'axe
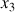avec la vitesse angulaire
.
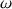La correspondance entre d'une part, le mouvement décrit ci-dessus par les équations d'Euler et d'autre part, les angles d'Euler et les résolutions précédemment présentés, concerne essentiellement la rotation
.
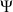Le moment cinétique total est conservé et noté
.
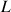L'inclinaison
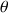de la toupie étant fixe, la vitesse de la rotation
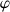valait :
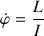
La vitesse angulaire autour de son axe propre est reliée à
par l'équation de projection :
.
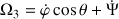Sachant que
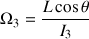, il vient que :
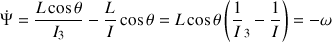
Au signe près, la rotation initiale autour de l'axe propre de la toupie fixe la pulsation de la précession, mesurée par les projections de la vitesse angulaire totale dans le plan
.
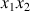Complément :
La conservation du moment cinétique total induit des vitesses de rotation d'Euler, d'amplitudes constantes, en mouvement harmonique et se composant selon la symétrie du solide.
Dans cette partie, le centre
est considéré comme fixe.
Si ce point est en mouvement, la translation est décrite par les équations pour l'impulsion.
