Conclusion
Avec les exemples considérés, la formulation d'Euler pour les rotations du solide paraît simple d'utilisation.
En effet lorsque les axes principaux (
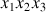) sont déterminés et les rotations réelles du solide identifiées par rapport aux rotations d'Euler (
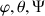), il reste à
déduire le vecteur rotation de composantes (
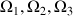) et appliquer les équations d'Euler, sans oublier les moments de forces à l'origine des rotations.
La toupie soumise à son poids et à la réaction du support (en
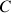) peut ainsi être traitée.
Le moment du poids ne peut avoir de composante selon l'axe
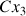, la composante du moment cinétique
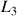est donc conservée et
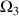est constante.
Pour les deux autres directions, si l'axe
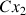est dans le plan contenant l'axe vertical
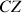, alors le moment du poids est porté par
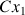et vaut
.
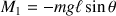Avec le formalisme lagrangien, l'étude est toujours plus directe et systématique.
