Centre de masse ou centre d'inertie
Pour calculer le moment cinétique total, il est utile de rafraîchir quelques propriétés générales relatives aux éléments du formalisme utilisé.
Dans un grain précédent, lors de la généralisation au système de points matériels, une propriété particulière du centre de masse (et centre d'inertie) était obtenue à partir de la composition des vitesses pour chaque particule
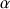soumise à un entraînement commun
.
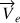En effet partant du rayon vecteur de chaque particule et de la relation de Chasles :
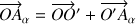
cette écriture permet de relier les mouvements d'un système de points
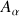décrit dans deux référentiels galiléens en translation rectiligne relative à la vitesse
.
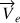La composition de vitesse pour chaque particule est déduite :
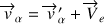
Le calcul de la quantité de mouvement totale est effectué et les impulsions totales mesurées dans chaque référentiel sont reliées entre elles :
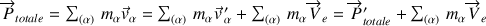
Cette relation est générale : les quantités de mouvement mesurées dans deux référentiels galiléens diffèrent par une quantité de mouvement, celle d'une particule dont la masse équivaut à la masse totale se déplaçant à la vitesse du référentiel mobile.
Cette formulation permet de déduire un point particulier du système : son centre d'inertie.
Syntaxe :
Le centre d'inertie est le centre du référentiel mobile dans lequel l'impulsion totale mesurée
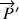est nulle.
Donc lorsque
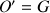, l'impulsion totale
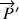est nulle
Explication : Centre d'inertie et centre de masse
Le centre d'inertie est le centre de masse.
En effet, la vitesse d'entraînement (celle du centre du référentiel mobile) correspond identiquement à celle du CDM, noté
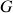, du système selon :
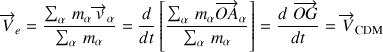
Ceci permet de déduire que, dans le référentiel du CDM, l'impulsion totale mesurée est toujours nulle.
Cette propriété avait déjà été avantageusement utilisée dans le problème à deux corps.
Si la quantité de mouvement, mesurée dans le référentiel mobile, est susceptible de simplifier un calcul, le choix du référentiel mobile s'imposera de lui-même.
