Moments d'inertie d'un cylindre plein
Le cylindre est un solide dont les symétries sont simples et explicites.
Ses axes principaux sont représentés sur la Fig. 5 a.
Le cylindre est plein et homogène, de rayon
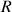, de hauteur
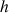et de masse
.
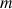Sa masse volumique est constante et notée
.
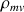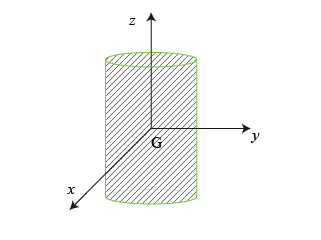
Pour aller au plus simple, le centre du repère est le CDM du cylindre.
Le calcul du moment d'inertie produit une intégrale volumique (
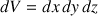) délimitée par la surface du solide.
Ainsi les coordonnées cylindriques sont adaptées telles que : la variable radiale,
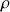, du plan
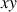varie de
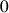à
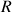, celle angulaire
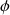de
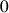à
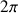et la côte
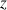de
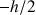à
.
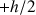Le volume total du cylindre est
.
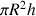L'axe principal du cylindre est
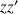et son moment d'inertie est :
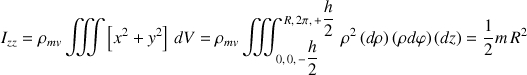
Les éléments d'intégration ont été mis en évidence par leur variation respective.
Le choix de coordonnées adaptées à la symétrie permet de séparer les
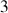intégrales.
Les deux autres directions propres correspondent aux axes de symétrie contenus dans le plan transverse à
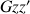passant par
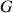; elles sont équivalentes et indiscernables en termes de rotation : les moments principaux,
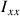et
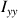, sont égaux.
De ce fait, une alternative au calcul direct est l'utilisation d'une propriété présentée ci-dessus : le moment d'inertie par rapport au centre du repère
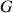, selon :
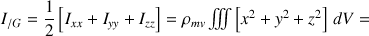
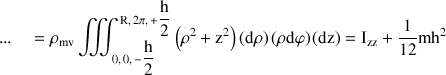
Ce qui permet de déterminer
.
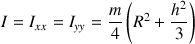Ces
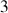axes sont des axes propres du cylindre et leurs moments d'inertie sont principaux.
Les termes hors diagonale du tenseur d'inertie sont identiquement nuls.
Complément : Quelques variantes.
Selon l'utilisation du cylindre, une translation des axes à la base ou sur une génératrice (cylindre qui roule) implique l'utilisation du théorème de Huygens pour calculer d'autres moments d'inertie.
Si le cylindre est complétement creux, les intégrales ci dessus sont des intégrales de surface.
La variable radiale vaut
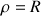, et les deux autres variables ont des variations inchangées pour décrire le pourtour du cylindre.Ainsi le moment d'inertie principal vaut
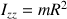et présente, à masse égale, un effet plus "inertiel" qu'un cylindre plein.Les deux autres moments principaux d'inertie sont calculés selon la même procédure décrite ci-dessus.
Pour un cylindre creux entre les rayons
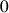et
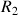, le calcul direct ci-dessus peut être reproduit avec la spécificité de la variation radiale suivante :
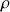varie entre
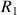et
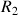.Il est utile de comparer le moment d'inertie
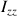avec celui d'un cylindre plein de rayon
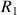et de masse
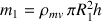dont a été déduit le moment du creux cylindrique (de masse volumique
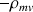) pour obtenir :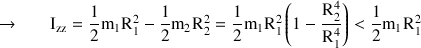
Sur ces quelques variantes, l'effet inertiel du cylindre est progressif du cylindre plein à celui creux en passant par l'épaisse bordure.
