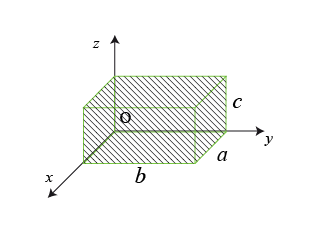
Tenseur d'inertie d'un parallélépipède.
Le parallélépipède est homogène (masse volumique
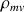constante), d'arêtes
,
,
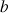de masse
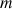dans un repère dont les axes sont fixés à un des sommets.
Le tenseur d'inertie n'est pas diagonal puisque ces axes ne sont pas ses axes de symétrie : les intégrales de fonctions impaires sont effectuées de
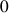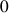à
,
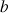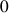à
,
à
respectivement et non pas de
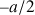à
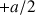, ..., ce qui n'annule pas les composantes hors diagonale. (Fig. 5c)
Les éléments du tenseur sont obtenus selon :
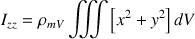
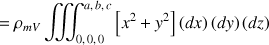
soit :
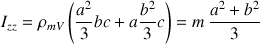
Avec le même type de calcul, les autres moments d'inertie valent :
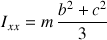et
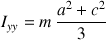
Et les termes non diagonaux :
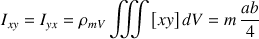
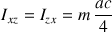
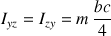
Ces trois derniers termes s'annulent donc lorsque les bornes deviennent symétriques.
De plus, les moments principaux par rapport au centre
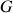du parallélépipède sont obtenus en appliquant le théorème de Huygens aux moments axiaux (et diagonaux) ci-dessus.
