Moments d'inertie d'un cône
La masse du cône est
. Sa hauteur est
et le rayon de base est
.
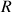Le volume du cône est le tiers de celui du cylindre : la méthode de calcul développée ci après permet de l'obtenir.
Les axes considérés dans le développement sont
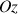, axe passant par le sommet
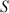du cône et perpendiculaire à la base et pour
ou
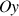dans le plan de la base, comme pour le cylindre, sont interchangeables (in-différentiables), ce qui laisse supposer une égalité des moments d'inertie.
L'équation du pourtour du cône est ici décrite par des cercles dont le rayon dépend de sa hauteur selon
, qui est l'équation de la génératrice du cône.
Les paramètres
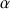et
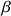dépendent du rayon de base
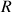et de la hauteur
selon
et
(tangente du demi angle au sommet).
Lors des intégrations sur le volume, les coordonnées cylindriques sont utilisées et l'intégrale s'effectue dans l'ordre suivant :
L'angle
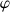varie de
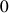à
,
Le rayon dans chaque plan paralèlle à la base
varie de
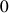à l'équation de la génératrice.
La hauteur
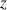varie de
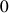à
.
Ces bornes d'intégration servent également à déterminer la position du CDM (sur l'axe
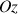à
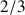du sommet
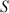) pour une évaluation des axes principaux d'inertie par le théorème de Huygens.
Le moment d'inertie selon
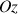est alors :
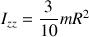valable quelle que soit l'origine sur l'axe.
Les deux autres moments d'inertie valent :
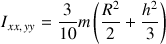
Attention :
Lorsque le cône est posé sur le sol et roule (Fig. 1a), l'axe de rotation principal est toujours l'axe du cône (
).
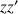La génératrice et axe instantané de rotation n'est pas parallèle à l'axe
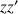et le théorème de Huygens ne peut être appliqué.
Le calcul du moment d'inertie par rapport à la génératrice peut être effectué directement en prenant la génératrice comme axe de référence. L'expression des contours du cône sont à adapter au choix des coordonnées.
Travailler dans le système des axes principaux reste la méthode la plus simple.
