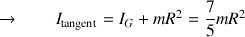Moments d'inertie d'une sphère.
La sphère est homogène de masse volumique
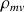; sa masse totale est
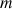et son rayon est noté
.
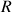Son volume vaut
.
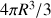Vu la symétrie de la sphère, trois rayons orthogonaux quelconques sont toujours axes principaux.
De plus les
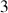moments d'inertie sont égaux,
.
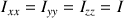Le centre du repère est confondu avec celui de la sphère ou CDM :
.
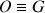Pour un calcul direct, le plus simple est d'utiliser les coordonnées sphériques et d'évaluer le moment d'inertie par rapport à un axe
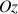vertical.
Évidemment, le calcul par rapport à l'axe
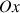ou
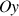devrait donner le même résultat.
Mais plus rapide est le calcul utilisant l'égalité des
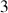moments d'inertie dans l'évaluation du moment d'inertie par rapport au point d'origine du repère :
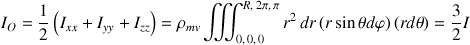
Cette relation permet de déduire
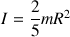
Complément :
L'égalité des
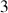moments d'inertie produit une indétermination de l'axe de rotation : celui-ci peut changer à tout moment.
Lors d'un roulement, le point de contact de la sphère avec le sol appartient à l'axe instantané de rotation, perpendiculaire à la direction du déplacement.
Dans ce cas le théorème de Huygens permet de déterminer le moment d'inertie par rapport à tout axe instantané tangent à la sphère pour obtenir :
