Moments d'une plaque plane rectangulaire
D'épaisseur négligeable (
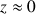), de cotés
(selon
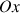) et
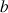, la plaque rectangulaire est homogène de densité surfacique
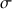et a une masse
.
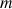Les moments d'inertie par rapport à des axes passant par son centre
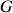et contenus dans son plan (
,
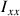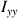) et perpendiculaire (
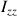) sont :
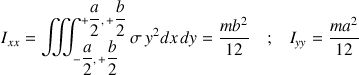
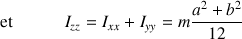
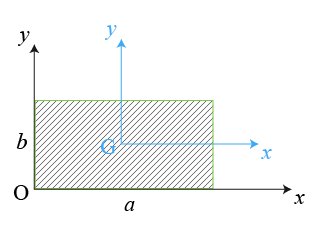
Le tenseur d'inertie exprimé dans le repère
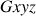est diagonal.
Pour s'en convaincre il suffit de calculer
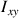et de remarquer que l'intégrale double est un produit de
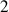intégrales simples, sur
et sur
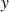, chacune d'une fonction impaire entre des bornes symétriques.
Le résultat de chaque intégration est une fonction paire qui s'annule du fait des bornes.
Complément :
Si la plaque est un pendule pesant tournant autour d'un de ses bords, ou une porte s'ouvrant en tournant sur un axe correspondant à un coté (
ou
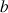), le moment d'inertie associé à cette rotation est obtenu par application du théorème de Huygens.
Par exemple
.
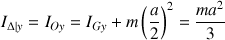Ce qui revient à effectuer l'intégration selon
entre
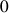et
.
Le tenseur n'est pas diagonal dans
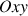, les bornes d'intégration n'étant plus symétriques.
