Contexte de l'exemple
La sphère de rayon
, de masse
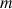et de moment d'inertie
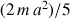, roule sans glisser sur un plan incliné d'un angle
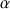par rapport à l'horizontale. (Fig. 9)
Elle roule sans glisser : une contrainte due au point de contact au sol, qui à tout instant est fixe, et qui produit une relation directe entre la rotation de la sphère et sa translation globale, réduisant le nombre de degrés de liberté.
Méthode : Analyse et notations
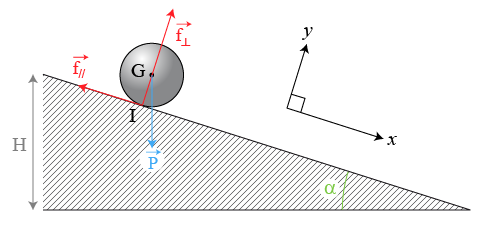
Si le mouvement de la sphère est rectiligne, une représentation de l'ensemble dans un plan vertical (
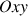) selon la Fig. 9 permet de poser les bases de l'énoncé.
Le CDM de la sphère est noté
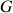et le point de contact avec le plan incliné est
.
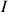Le roulement de la sphère est produit par un contact particulier au niveau du point
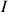: une adhérence entre les deux surfaces produit une réaction du support avec les deux composantes suivantes
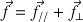. (Voir chap. III)
Outre la translation de son centre de masse, la sphère évolue selon un seul degré de liberté : la rotation, notée
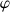, autour d'un axe perpendiculaire au plan
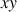de la Fig. 9.
La condition de roulement sans glissement peut être déduite de deux façons :
Intuitivement, elle implique un déplacement
du CDM correspondant exactement à l'arc de cercle produit par la rotation de la sphère soit :
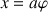ou encore en termes de vitesses
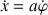.Une méthode plus élaborée, systématique et rigoureuse permet d'obtenir cette condition en notant que le point de contact
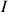est un point de l'axe instantané de rotation de la sphère et que sa vitesse instantanée « absolue »
est nulle.
La position de
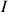dans le repère fixe s'écrit
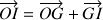permettant le passage par le centre de masse
.
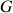Le mouvement de I dans le référentiel mobile de centre
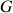est une rotation pure et la vitesse du point
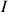est le résultat d'une composition de deux mouvements :
.
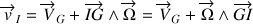La vitesse instantanée du point I étant nulle, cette propriété permet d'écrire
.
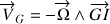Le vecteur vitesse rotation est porté par l'axe perpendiculaire au plan du mouvement de chaque point (
).
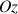La rotation produit un mouvement de
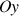vers
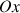: son vecteur vitesse rotation s'écrit
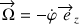, de sorte que :
.
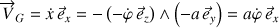Le résultat intuitif est retrouvé.
Les éléments communs au mouvement étant mis en place, les différentes résolutions peuvent être à présent développées selon
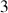méthodes.
