Résolution par le formalisme lagrangien
Le lagrangien de la sphère en mouvement s'exprime en fonction des énergies cinétique et potentielle de pesanteur à l'origine du mouvement.
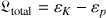
L'énergie cinétique de la sphère est la somme de celle de translation du CDM et de celle de rotation de la sphère autour de son axe propre, en tenant compte de la contrainte de roulement sans glissement :
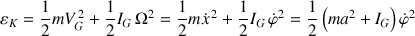
Ainsi une application du théorème de Huygens permet la translation de l'axe de rotation passant par
vers un axe instantané qui lui est parallèle, passant par une tangente à la sphère et donc par le contact au sol
.
L'énergie potentielle de la sphère est celle de la pesanteur, portée par le poids de la sphère, lequel est appliquée au centre de masse
.
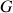Elle s'écrit
.
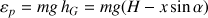Avec une seule variable, l'équation du mouvement se déduit aisément du formalisme lagrangien :
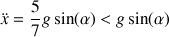
Elle met ainsi en évidence une accélération inférieure à la valeur obtenue pour le point matériel.
La différence provient d'une "inertie plus grande" due à la rotation : celle-ci consomme une partie de l'énergie disponible pour l'ensemble du mouvement, réduisant d'autant celle de la translation globale.
