Description des rotations d'Euler
L'animation Flash ci dessous permet de définir successivement
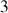 angles de rotation,
angles de rotation,
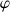 ,
,
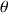 et
et
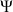 définis par Euler pour décrire la composition de rotations la plus générale que puisse décrire un solide dans l'espace :
définis par Euler pour décrire la composition de rotations la plus générale que puisse décrire un solide dans l'espace :
En résumé à l'animation et partant d'un état initial du solide, décrit par le système d'axes propres
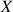 ,
,
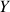 ,
,
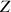 de centre
de centre
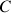 :
:
La 1ère rotation met en jeu l'angle
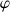 , variant de
, variant de
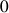 à
à
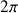 .
.Elle s'effectue à la vitesse angulaire
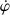 , autour de l'axe
, autour de l'axe
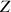 et donne un système d'axes intermédiaire :
et donne un système d'axes intermédiaire :
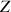 ,
,
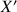 et
et
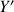 .
. C'est le premier état intermédiaire du solide.
Il s'agit de la rotation de précession dans le cas de la toupie symétrique traitée précédemment.
La seconde rotation, à l'origine de la nutation qui sera vue plus loin dans ce chapitre, s'effectue à la vitesse angulaire
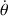 autour du nouvel axe
autour du nouvel axe
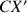 .
. L'inclinaison
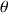 représentée est comprise entre
représentée est comprise entre
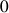 et
et
 .
. Elle laisse invariante l'axe de rotation mais transforme les axes
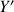 et
et
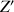 en
en
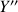 et
et
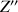 .
.Le second état intermédiaire est ainsi obtenu.
L'effet de cette rotation est de soulever le plan initial (perpendiculaire à la première rotation).
La droite
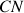 est la ligne nodale (précédemment
est la ligne nodale (précédemment
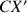 ).
).
La troisième et dernière rotation est notée
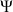 et a lieu autour de l'axe
et a lieu autour de l'axe
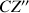 avec une variation angulaire comprise entre
avec une variation angulaire comprise entre
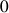 à
à
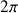 .
.Cette rotation produit les axes du référentiel mobile
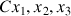 , idéalement les axes propres du solide.
, idéalement les axes propres du solide. C'est une rotation propre car elle a lieu autour d'un axe qui est souvent un axe principal du solide.
Cet état décrit le mouvement instantané de rotation du solide, somme des
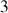 rotations qui le constituent.
rotations qui le constituent.
La vitesse angulaire totale est la somme vectorielle des vitesses angulaires issues des trois rotations d'Euler.
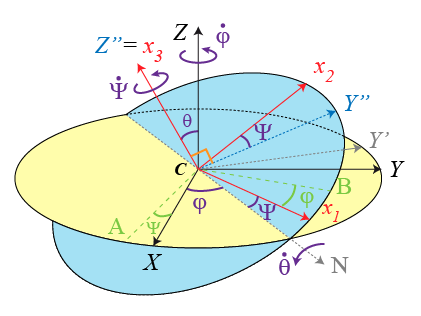
Pour exprimer cette vitesse dans l'espace d'arrivée
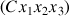 , il convient d'exprimer chaque rotation dans cet espace puis d'en effectuer la somme, composante à composante.
, il convient d'exprimer chaque rotation dans cet espace puis d'en effectuer la somme, composante à composante.
Attention :
Sur la figure 14 sont également représentés les éléments (points
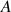 et
et
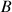 ) permettant de démontrer ultérieurement le théorème d'Euler
) permettant de démontrer ultérieurement le théorème d'Euler





