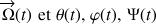Angles d'Euler et vitesse angulaire totale.
Avant de sommer les vitesses angulaires, il faut toutes les exprimer dans le référentiel mobile.
Les grandeurs indicées se rapportent donc à l'espace des axes mobiles
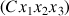et la projection de chaque vitesse angulaire donne lieu aux expressions suivantes :
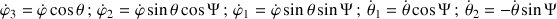
La projection de la dernière rotation est évidente
Définition :
La base des trois rotations d'Euler (
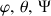), étant définies pour représenter les rotations les plus générales qu'un solide puisse décrire, la vitesse angulaire totale
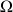du solide s'écrit :
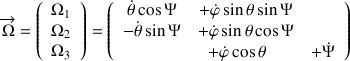
Elle est exprimée dans le référentiel mobile
.
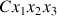Pour décrire le mouvement d'un solide, en général ces rotations dépendent du temps, condition nécessaire pour avoir une vitesse angulaire et un moment cinétique associé.
Ainsi pour être rigoureux, il eut fallu écrire :
