Le théorème d'Euler (1776)
Pour démontrer ce théorème il faut chercher le diamètre invariant par les trois rotations.
Pour les besoins de la démonstration, la ligne nodale (et sa représentation sur les plan-cercles : le point
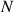) constitue une référence.
Cette ligne est invariante par la rotation
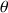mais elle subit les deux autres rotations
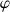et
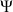. Il faut donc chercher l'axe de rotation qui réalise ces deux rotations sur
.
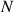Deux autres points sont alors nécessaires, l'un sur le plan (et cercle ou sphère) initial et l'autre sur le plan (et cercle ou sphère) final.
En effet, de part et d'autre de la ligne nodale et de
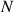, il est possible de construire
Sur le plan-cercle initial, le point
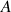déduit par rotation de l'axe
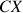, d'un angle
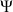opposé au sens trigonométrique, autour de l'axe vertical
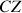(Fig.14).Ce point
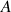produit
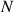lorsque les deux rotations
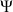et
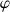lui sont appliquées, rotations autour de l'axe
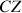.Sur le plan-cercle d'arrivée, le point
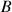est obtenu par rotation de l'axe
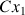, d'un angle
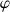dans le sens trigonométrique, autour de l'axe
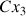(Fig.13). Cette fois, les deux rotations
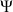et
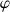sont appliquées à
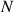pour obtenir le point
.
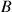Ces deux points caractérisent la double rotation,
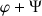, de part et d'autre de la ligne nodale.
Les arcs
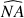et
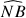sont égaux.
Les deux axes de rotation étant perpendiculaires à la ligne nodale, les deux points
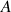et
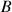sont ‘symétriques' par rapport au point
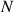dans une rotation par rapport à un axe intermédiaire à
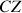et
.
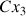Le point
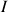recherché est situé sur la sphère de centre
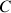et sur le diamètre invariant (aux 3 rotations successives) ; il doit être invariant lors des mouvements d'arcs
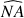et
.
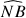Il appartient alors à la bissectrice (au plan bissecteur) de l'angle
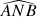ce qui permet de vérifier les égalités d'arcs et d'angles mettant en jeu les points
,
,
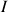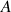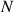et
.
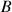Les trois rotations d'Euler permettent ainsi une démonstration aisée du théorème d'Euler.
À présent, quelques applications directes de ces rotations peuvent être développées.
