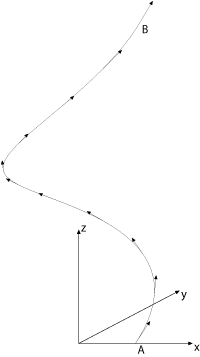
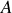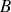Dans le cas d'une intégration le long d'une courbe (calcul d'une circulation) entre deux points et , si cette courbe est paramétrée par trois fonctions

Figure 4: Lacet gauche

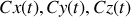
en fonction d'un paramètre quelconque 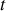(par exemple le temps définissant la position d'un mobile) l'élément de longueur correspond à la direction du vecteur tangent à la courbe exprimé en fonction de l'abscisse curviligne 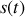. Cette dernière, correspondant à la distance parcourue par le mobile par exemple, est obtenue par

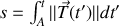
où 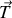est le vecteur tangent à la courbe

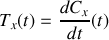
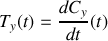
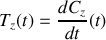
(dans le cas du mobile le vecteur vitesse).

Pour résumer, il faut donc dans l'ordre calculer le vecteur vitesse, sa norme, intégrer ce résultat pour obtenir l'abscisse curviligne 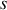, prendre la réciproque (si elle existe) de la formule obtenue pour trouver 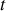en fonction de 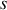, et enfin ré-exprimer 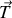en fonction de 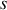puis le normaliser.

En pratique on rencontrera surtout deux cas : la droite pour laquelle par exemple

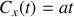
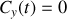
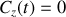
puisque nous pouvons orienter arbitrairement notre système de coordonnées en l'absence d'autres contraintes on obtient donc

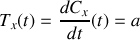
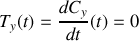
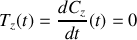
puis

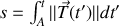
donc trivialement

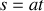
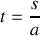
et enfin

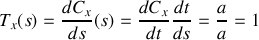
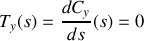
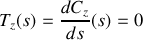
donc ce vecteur est bien normalisé à 1 et sa direction est celle que nous attendions.

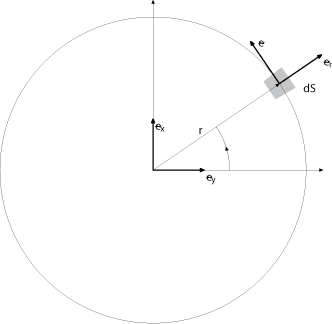
Dans le cas du cercle en deux dimensions on peut prendre

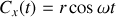
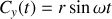
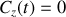
on obtient donc

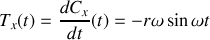
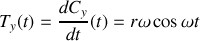
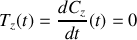
puis

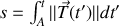
donc

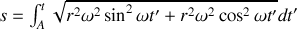
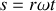
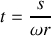
et enfin

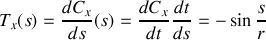
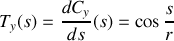
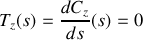
donc là encore ce vecteur est bien normalisé à 1 et sa direction orthoradiale est celle que nous attendions.

Figure 5: Vecteur vitesse tangent au cercle de rayon r parcouru à vitesse constante