Le paragraphe précédent nous montre que dans le cas du cercle, il peut être avantageux de travailler dans d'autres systèmes de coordonnées que les cartésiennes orthonormées directes traditionnelles. En fait, nous verrons que les coordonnées cartésiennes servent surtout en physique à traiter les cas généraux, les cas mono-dimensionnels, ou à établir des relations, mais souvent les problèmes étudiés présentent des symétries telles qu'il vaudra mieux se placer en coordonnées de type polaire.

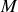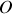À deux dimensions on repère un point par sa distance à l'origine et par l'angle 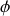que fait le vecteur 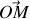avec le vecteur 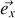d'une base cartésienne de référence.

Dans ce cas on a 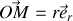où 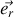est dit vecteur radial, et le vecteur 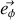obtenu après une rotation de 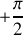qui lui est orthogonal est dit vecteur orthoradial, c'est celui que nous avons trouvé par le calcul comme élément de longueur à la question précédente.

On obtient ainsi par exemple dans ce système de coordonnées la longueur 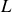(ou périmètre) du cercle par intégration. Le paramètre valant 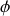on trouve

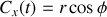
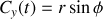
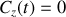
et

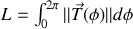
donc comme au paragraphe précédent (en plus simple)

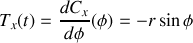
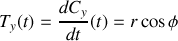
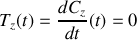
puis

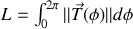
donc

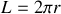
résultat que nous attendions.

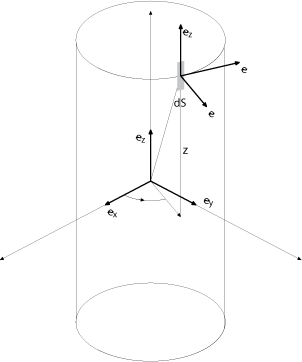
Dans la suite nous noterons .

Figure 6: Coordonnées sphériques

Figure 7: Coordonnées cylindriques

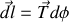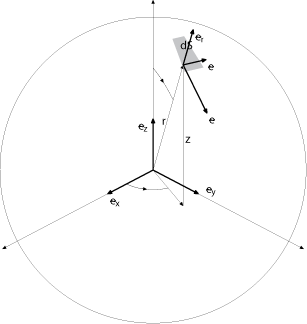
Il y a deux façons de passer à trois dimensions : soit on reprend la coordonnée 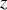des cartésiennes et on obtient le système de coordonnées appelées cylindriques, 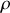notant désormais la distance à l'origine de la projection 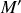de 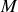sur le plan 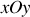, soit on introduit l'angle 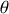(colatitude) du vecteur 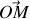avec le vecteur 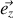et l'on obtient les coordonnées dites sphériques. Le nom de ces différents systèmes de coordonnées doit vous donner une idée du type de situation où elles sont le plus pertinentes. Par exemple sur Terre on repère les mobiles par leur altitude (correspondant à ) et par leur latitude et longitude.