Dans le paragraphe précédent nous avons vu comment trouver l'élément de longueur dans un système de coordonnées arbitraires curvilignes. Ceci nous a permis de calculer des circulations.
De même pour calculer des flux ou des intégrales volumiques il nous faut transformer les coordonnées cartésiennes dans les nouveaux systèmes de coordonnées.
Ainsi pour calculer la surface
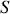 d'un carré de côté
d'un carré de côté
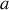 en cartésiennes (sans doute le cas le plus simple)
en cartésiennes (sans doute le cas le plus simple)
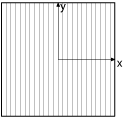
on écrit en général en se plaçant dans un système de coordonnées approprié
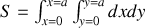
et en choisissant par exemple d'intégrer d'abord sur
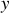
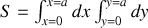
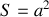
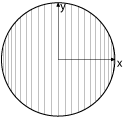
Par contre si nous envisageons de même de calculer la surface d'un cercle de rayon
 la situation se complique fortement car si nous choisissons d'intégrer par exemple d'abord sur
la situation se complique fortement car si nous choisissons d'intégrer par exemple d'abord sur
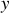 les bornes d'intégration varient avec la position
les bornes d'intégration varient avec la position
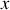
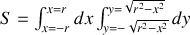
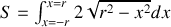
en faisant le changement de variable
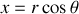
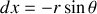
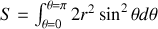
en linéarisant
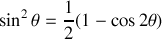 on a
on a
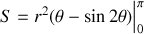
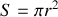
Reconnaissons que cette méthode est un peu compliquée et qu'elle nous a obligés de toute façon à introduire une variable trigonométrique.
Si désormais nous passons en coordonnées polaires
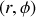 pour le cercle
pour le cercle
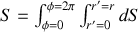
On peut montrer mathématiquement que l'élément de surface
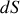 est égal au déterminant de la matrice dite jacobienne, formée des dérivées des anciennes coordonnées par rapport aux nouvelles. Ce déterminant est égal à la norme du produit vectoriel des dérivées partielles des fonctions paramétrisant la surface.
est égal au déterminant de la matrice dite jacobienne, formée des dérivées des anciennes coordonnées par rapport aux nouvelles. Ce déterminant est égal à la norme du produit vectoriel des dérivées partielles des fonctions paramétrisant la surface.
Ainsi comme
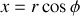
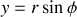
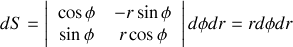
graphiquement on peut voir cet élément comme un petit carré tangent au cercle de dimensions longitudinales
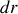 suivant
suivant
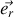 et
et
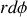 suivant
suivant
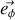
finalement
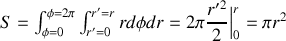
Remarque :
Notons bien que dans tous les cas l'élément de surface
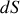 est bien homogène à une surface car par exemple
est bien homogène à une surface car par exemple
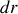 est homogène à une longueur.
est homogène à une longueur.
Notons également que vectoriellement l'élément de surface
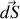 est normal à la surface
est normal à la surface
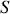 et de préférence, par convention, orienté vers l'extérieur de la surface s'il y en a un pour une surface fermée. Pour une surface ouverte dans l'espace direct, la règle du tire-bouchon (de droitier) donne à partir d'un choix du sens de parcours du périmètre de la surface l'orientation algébrique de celle-ci. En pratique nous ne rencontrerons jamais ce problème.
et de préférence, par convention, orienté vers l'extérieur de la surface s'il y en a un pour une surface fermée. Pour une surface ouverte dans l'espace direct, la règle du tire-bouchon (de droitier) donne à partir d'un choix du sens de parcours du périmètre de la surface l'orientation algébrique de celle-ci. En pratique nous ne rencontrerons jamais ce problème.
De même si nous passons au calcul de volumes, sauf sur les parallélépipèdes l'intégration en cartésiennes peut être très pénible si nous extrapolons à une dimension supplémentaire les difficultés que nous avons eues dans l'exemple précédent.
Par contre dans les systèmes de coordonnées adaptées à la forme de l'objet l'intégration sera plus aisée. Retenons l'expression de l'élément de volume en cartésiennes
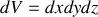
La procédure de calcul d'une intégrale volumique étant la même que pour le calcul d'une intégrale surfacique : intégration entre les bornes définissant l'objet suivant trois directions successives.
En cylindriques on déduit facilement l'élément de volume du cas bidimensionnel des coordonnées polaires
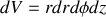
(cube élémentaire de hauteur
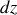 )
)
par contre en sphériques il faut de nouveau calculer le déterminant de la matrice jacobienne des dérivées partielles et on trouve
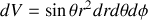
En effet sur la sphère la taille d'un cercle contenu dans un plan orthogonal à
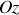 (plan horizontal) diminue avec la latitude.
(plan horizontal) diminue avec la latitude.
On en déduit l'élément de surface de la sphère dans ces coordonnées
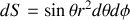
ou vectoriellement
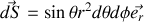
et grâce à ces deux relations nous pouvons retrouver surface
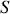 et volume
et volume
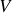 d'une sphère
d'une sphère
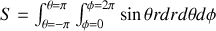
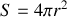
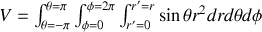
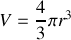
résultats que nous connaissions depuis longtemps en principe.



