Énoncé
L'une des extrémités d'un ressort, de constante de raideur
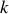 et de longueur à vide
et de longueur à vide
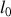 , est accrochée à un support vertical fixe. On vient attacher à l'autre extrémité un bloc de masse
, est accrochée à un support vertical fixe. On vient attacher à l'autre extrémité un bloc de masse
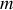 posé sur un support plat horizontal.
posé sur un support plat horizontal.
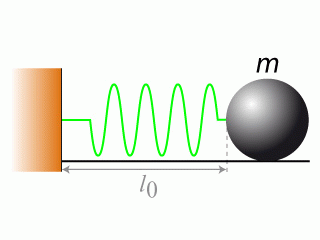
Le bloc est écarté d'une distance
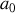 de sa position d'équilibre. Il est ensuite lâché sans vitesse initiale. Les forces de frottement sont négligées.
de sa position d'équilibre. Il est ensuite lâché sans vitesse initiale. Les forces de frottement sont négligées.1.a) En utilisant les lois de Newton, déterminer l'équation différentielle régissant l'évolution du mouvement du bloc.
1.b) Retrouver ce résultat en vous appuyant sur des considérations énergétiques.
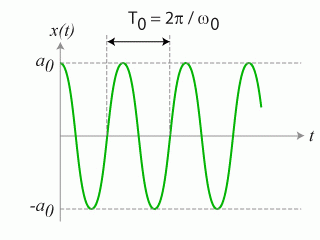
Résoudre l'équation différentielle et représenter de manière schématique l'évolution temporelle de la position du bloc.
1.a) Appliquer le principe fondamental de la dynamique sur la masse
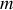 .
.1.b) Appliquer le théorème de l'énergie cinétique (ou la conservation de l'énergie mécanique) sur la masse
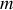 .
.Résoudre l'équation différentielle (voir boite à outils) et déterminer les constantes d'intégration à partir des conditions initiales.
1.a) Appliquer le principe fondamental de la dynamique sur la masse
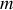 :
:
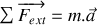
Projeter sur l'axe horizontal d'origine
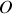 sachant que, si la masse à un instant quelconque est repérée par le point
sachant que, si la masse à un instant quelconque est repérée par le point
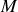 ,
,
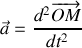 et que la loi de Hooke donne la tension du ressort
et que la loi de Hooke donne la tension du ressort
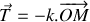 .
. 1.b) Appliquer le théorème de l'énergie cinétique sur la masse
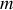 :
:
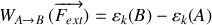 (ou la conservation de l'énergie mécanique :
(ou la conservation de l'énergie mécanique :
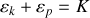 ).
). La seule force extérieure appliquée au système qui travaille est la tension du ressort
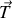 .
.On appliquera le théorème par exemple entre la position initiale (
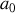 ) et une position quelconque (
) et une position quelconque (
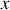 ).
).Résoudre l'équation différentielle (voir boite à outils) et déterminer les constantes d'intégration à partir des conditions initiales à
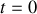 :
:
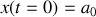 et
et
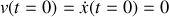 .
.
Voir le cours sur les systèmes oscillants d'université en ligne : http://www.uel.education.fr/consultation/reference/physique/syst_oscillants/index.htm
Faire un schéma clair faisant apparaître les forces mises en jeu.
Préciser le référentiel dans lequel le système est étudié en y attachant un repère judicieusement choisi.
Donner (lorsqu'elle est connue) l'expression des forces mises en jeu dans le référentiel d'étude en précisant clairement les lois utilisées si nécessaire (loi de Hooke pour la tension d'un ressort par exemple).
Ecrire l'équation différentielle vectorielle à partir d'une loi de Newton correctement énoncée.
Projeter correctement (sans bricolage sur les signes !) l'équation vectorielle sur les axes.
Résoudre l'équation différentielle scalaire.
Résolution d'une équation différentielle linéaire du second ordre à coefficients constants, de forme générale :
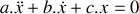 .
.
L'expression de la solution générale
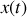 se déduit de la résolution de l'équation, que l'on suppose connue.
se déduit de la résolution de l'équation, que l'on suppose connue.
On rappelle que le discriminant de l'équation caractéristique associé à l'équation différentielle s'écrit :
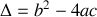 . Comme pour une équation du second degré, on a alors trois cas possibles pour
. Comme pour une équation du second degré, on a alors trois cas possibles pour
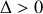 ,
,
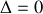 ou
ou
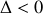 .
.
Pour un oscillateur harmonique,
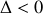 avec
avec
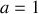 ,
,
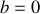 et
et
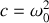 . La résolution dans ce cas montre que
. La résolution dans ce cas montre que
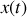 , en notation réelle, s'écrit sous l'une des trois formes équivalentes suivantes :
, en notation réelle, s'écrit sous l'une des trois formes équivalentes suivantes : 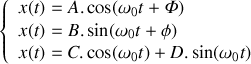
Pour un oscillateur harmonique amorti
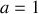 ,
,
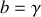 et
et
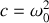 , d'où
, d'où
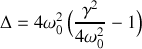 .
. La résolution dans les trois cas possibles montre que
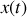 , en notation réelle, s'écrit sous l'une des formes équivalentes suivantes :
, en notation réelle, s'écrit sous l'une des formes équivalentes suivantes : a)
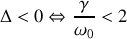 , alors :
, alors :
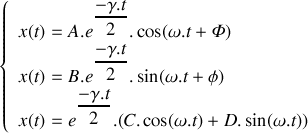
avec
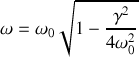
b)
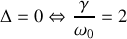 , alors :
, alors :
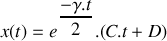
c)
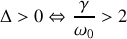 , alors :
, alors :
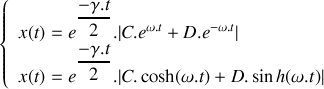
avec
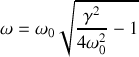
On constate que
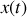 dépend de deux constantes d'intégration
dépend de deux constantes d'intégration
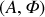 ,
,
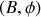 ou
ou
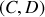 . Il faut se donner deux relations pour les déterminer. La solution est alors unique. Dans un problème physique, ces deux relations décrivent l'état initial du système à
. Il faut se donner deux relations pour les déterminer. La solution est alors unique. Dans un problème physique, ces deux relations décrivent l'état initial du système à
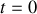 ; elles sont appelées conditions initiales
; elles sont appelées conditions initiales
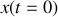 et
et
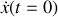 .
. Pour un oscillateur forcé (ou si l'origine du repère ne correspond pas à la position d'équilibre), le second membre de l'équation différentielle est non nulle. La solution est alors la somme d'une solution de l'équation particulière
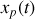 et d'une solution de l'équation caractéristique
et d'une solution de l'équation caractéristique
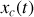 :
: 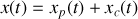
- La solution particulière
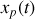 est de la forme du second membre ; s'il est une constante,
est de la forme du second membre ; s'il est une constante,
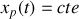 ; s'il est de forme sinusoïdale,
; s'il est de forme sinusoïdale,
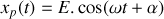 ; etc.
; etc. - La solution de l'équation caractéristique
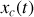 est celle de l'équation différentielle sans second membre et dépend alors du signe du discriminant comme décrit précédemment.
est celle de l'équation différentielle sans second membre et dépend alors du signe du discriminant comme décrit précédemment.
1.a) En appliquant le principe fondamental de la dynamique sur la masse
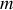 , avec la loi de Hooke (
, avec la loi de Hooke (
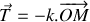 ) et après projection sur l'axe horizontal, on obtient :
) et après projection sur l'axe horizontal, on obtient : 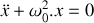 avec
avec
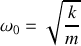 où
où
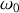 est la pulsation propre.
est la pulsation propre.1.b) En appliquant la conservation de l'énergie mécanique et en dérivant par rapport au temps, on obtient :
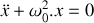 avec
avec
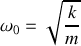
Une solution réelle est de la forme :
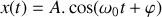
Les conditions initiales donnent :
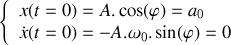
soit :
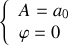
D'où :
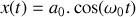 .
.
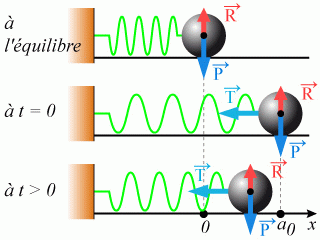
1.a) En appliquant le principe fondamental de la dynamique sur la masse
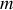 , il vient :
, il vient : 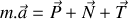
La loi de Hooke donne
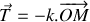
Avec
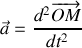 :
: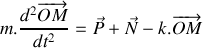
Avec
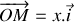 et après projection sur l'axe horizontal
et après projection sur l'axe horizontal
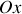 , on obtient :
, on obtient : 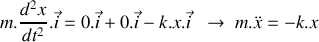
Finalement :
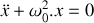 avec
avec
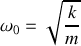 où
où
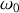 est la pulsation propre.
est la pulsation propre. 1.b) En appliquant le théorème de l'énergie cinétique à la masse
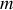 , il vient :
, il vient : 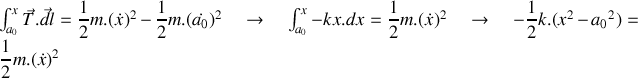
En dérivant par rapport au temps :
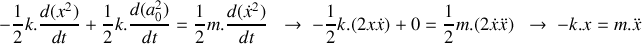
Finalement :
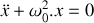 avec
avec
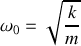
Une solution réelle est de la forme :
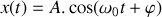 où
où
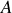 et
et
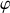 sont les constantes d'intégration à déterminer à partir des conditions initiales.
sont les constantes d'intégration à déterminer à partir des conditions initiales. La vitesse est obtenue en dérivant
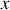 par rapport au temps :
par rapport au temps : 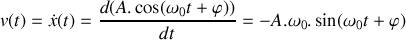
Les conditions initiales donnent :
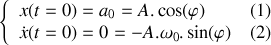
Dans l'équation (2),
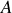 et
et
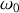 sont forcement non nulles (sinon, il n'y a pas d'oscillations), donc
sont forcement non nulles (sinon, il n'y a pas d'oscillations), donc
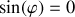 , soit
, soit
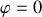 .
. Alors, avec
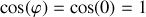 , l'équation (1) donne :
, l'équation (1) donne :
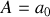 .
. D'où :
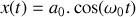 .
.




