Oscillateurs linéaires ; oscillateurs couplés - Exemple d'amortissement critique, suspension d'un véhicule

Oscillateurs linéaires ; oscillateurs couplés

Exemple d'amortissement critique, suspension d'un véhicule

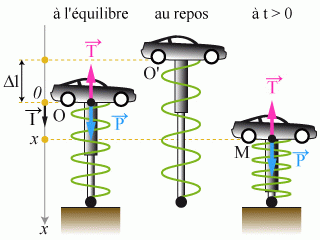
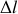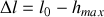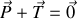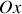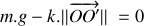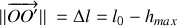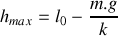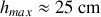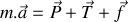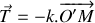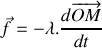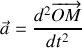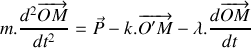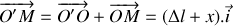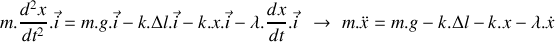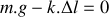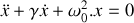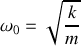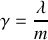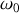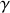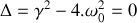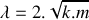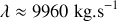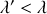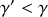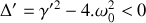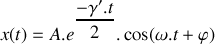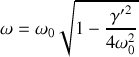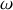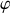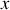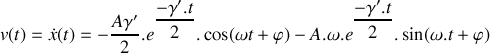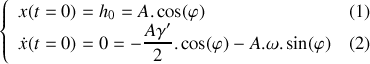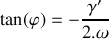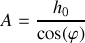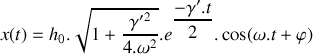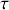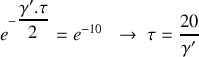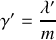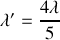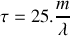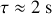Énoncé

On considère un véhicule de masse 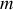. Le système de suspension de ce véhicule peut être représenté par l'association d'un ressort, de constante de raideur 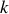et de longueur à vide 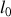, et d'un amortisseur provoquant une force de frottement de type fluide .

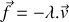Toute autre source de frottements est négligée.

Figure 1 : schéma équivalent du dispositif.

En supposant que le véhicule ne change pas d'altitude, déterminer la profondeur maximale 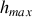d'un nid de poule à partir de laquelle les roues ne sont plus en contact avec le sol. On négligera le poids du système de suspension et des roues.
Etablir l'équation différentielle du mouvement vertical du véhicule lorsqu'il est écarté de sa position d'équilibre.
Déterminer le coefficient 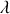pour que le régime d'amortissement soit critique.
L'usure des amortisseurs due au temps entraîne une diminution du coefficient 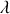d'un cinquième de sa valeur initiale :
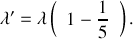
Qualifier le régime d'amortissement dans ce cas.
Un trou dans la chaussée écarte le ressort de sa position d'équilibre d'une longueur 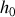. En considérant que la vitesse verticale est nulle en 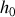, résoudre l'équation différentielle régissant l'évolution du mouvement vertical du véhicule. Déterminer le temps nécessaire pour que les oscillations du véhicule deviennent négligeables. Conclusion.

Applications numériques : ; ; ;

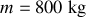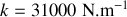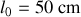On considérera les oscillations du véhicule négligeables lorsque leur amplitude maximale est divisée par un facteur .

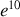Aide simple

Solution détaillée

Figure 2 : schéma du dispositif avec bilan des forces dans un référentiel galiléen.

Si on néglige le poids des roues, la situation pour laquelle celles-ci ne sont plus en contact avec le sol correspond au ressort dans sa position de repos, soit de longueur . Il faut donc déterminer la variation de longueur liée au poids du véhicule (situation à l'équilibre).
On obtient alors avec .
En appliquant le principe fondamental de la dynamique sur le véhicule à l'équilibre, il vient :

Après projection sur l'axe vertical , on obtient :

Finalement, avec : .
A.N. :
En appliquant le principe fondamental de la dynamique sur le véhicule, il vient :

La loi de Hooke donne
La force de frottement visqueux s'écrit :
Avec :

Avec , et après projection sur l'axe horizontal , on obtient :

Or, (voir question 1)
Finalement :
avec et où est la pulsation propre et est le taux d'amortissement.
Le régime d'amortissement critique correspond à un discriminant de l'équation caractéristique associé à l'équation différentielle nulle, soit :
(voir boite à outils de l'exercice de référence : Oscillateur harmonique mécanique horizontal (exercice 1) ).
Alors, avec et :
A.N. :
Avec , et est inchangée, alors . Le système passe donc dans un régime oscillatoire amorti.
Une solution réelle est de la forme : avec où est la pseudo-pulsation.
(voir boite à outils de l'exercice de référence : Oscillateur harmonique mécanique horizontal (exercice 1) ).
et sont les constantes d'intégration à déterminer à partir des conditions initiales.
La vitesse est obtenue en dérivant par rapport au temps :

Les conditions initiales donnent :
D'après l'équation (2), .
D'après l'équation (1), .
Avec :
D'où : ,
avec et .
Le temps à partir duquel les oscillations sont négligeables correspond à : .
Avec et :
A.N. :

Même si les amortisseurs n'ont perdu qu'un cinquième de leur taux d'amortissement, le temps d'oscillation du véhicule est suffisamment long pour rendre sa conduite dangereuse. Il est donc temps de les changer !