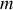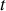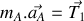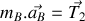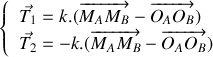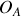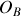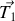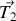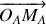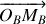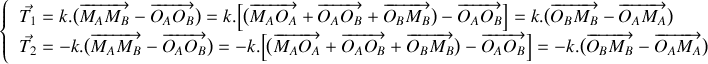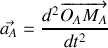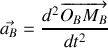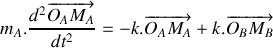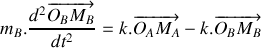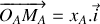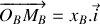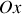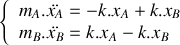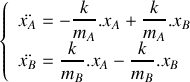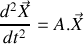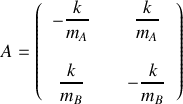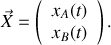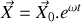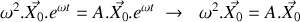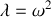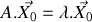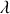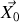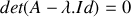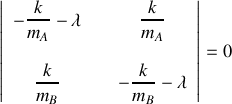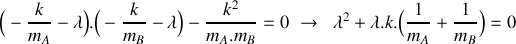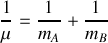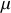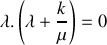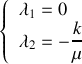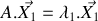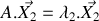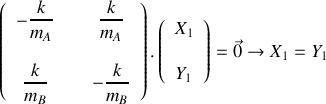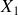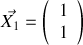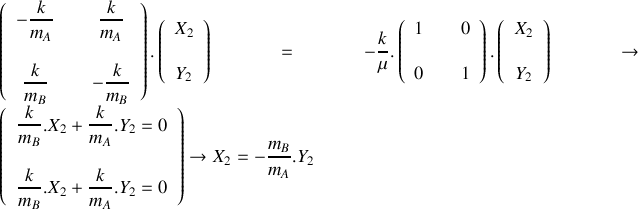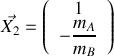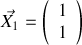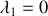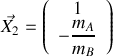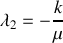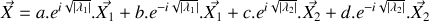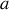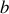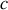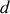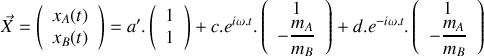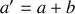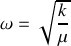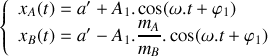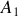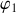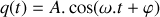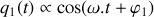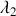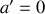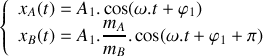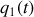Oscillateurs linéaires ; oscillateurs couplés - Vibration d'une molécule diatomique

Oscillateurs linéaires ; oscillateurs couplés

Vibration d'une molécule diatomique

Énoncé

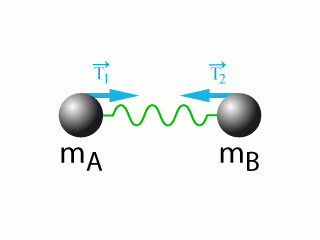
Pour étudier les modes de vibrations longitudinales d'une molécule diatomique 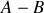, on assimile la liaison entre les deux atomes à un ressort de raideur 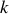. On désignera par 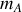et 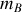les masses respectives des atomes 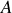et 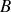. On notera par 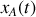et 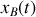les déplacements respectifs des atomes 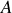et 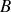par rapport à leur position d'équilibre.

On admet que la molécule n'est pas animée d'un mouvement de translation et que le poids des atomes est négligeable devant la tension du ressort. La masse du ressort simulant la liaison est négligeable et on suppose que l'amplitude de déplacement des deux atomes est toujours suffisamment faible pour que la loi de Hooke soit vérifiée. Finalement, tous les frottements sont considérés comme négligeables.

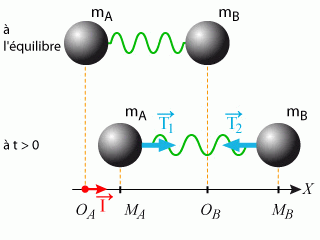
Schéma du système avec bilan des forces dans un référentiel galiléen

Etablir le système d'équations différentielles gouvernant l'évolution de la position des deux atomes dans le temps.
En vous appuyant sur la forme vectorielle du système d'équations différentielles obtenu à la question 1 : 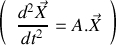, déterminer les valeurs propres et les vecteurs propres de la matrice .
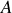Déduire du résultat de la question 2 la solution générale du système d'équations du mouvement.
Préciser le ou les mode(s) propre(s) de vibration du système d'oscillateurs et donner la ou les pulsation(s) propre(s) de vibration du système.
Donner la signification physique du ou des mode(s) propre(s) de la molécule en indiquant sur un schéma l'état de vibration correspondant.

Aide simple

Solution détaillée

En appliquant le principe fondamental de la dynamique à quelconque, il vient :
- Pour : .
- Pour : .
La loi de Hooke donne :
Afin d'obtenir l'équation du mouvement dans les repères d'origine et , il faut exprimer et en fonction de et/ou :

Avec et :
- Pour : .
- Pour : .
, et après projection sur l'axe horizontal , on obtient :
En divisant par et les équations obtenues à la question 1, on obtient :

Sous forme vectorielle, ce système s'écrit , avec :
et
On cherche alors une solution réelle de la forme
En dérivant deux fois cette solution par rapport au temps et en remplaçant dans l'équation vectorielle, il vient :

En posant , on a alors un problème aux valeurs propres avec valeur propre de et vecteur propre de .
Pour déterminer les valeurs propres, il faut résoudre : .

D'où :
On pose ( est alors la masse réduite du système) :

On a alors une équation du second degré avec deux solutions possibles : . Ce sont les valeurs propres de .
Pour déterminer les vecteurs propres, il faut résoudre : et .
Ici : ( , et étant forcément non nulles).
On choisit en général l'unité pour la valeur de , soit :
De la même façon :

Soit :
On a alors :
- le vecteur propre associé à la valeur propre
- le vecteur propre associé à la valeur propre
La solution générale du système d'équations est de la forme . Avec , il s'agit d'une combinaison linéaire des solutions aux valeurs propres telle que :
où , , et sont des constantes.
Ici : avec et
D'où : où et sont les constantes d'intégration.
Le mouvement peut être décomposé en une superposition (somme) de mouvements harmoniques appelés modes propres (ou modes normaux) de vibration.
On reconnaît ici la solution d'un oscillateur harmonique du type . Dans le cas présent, il n'y a qu'une seule solution de cette forme dans et .
Le seul mode propre du système est alors :
avec sa pulsation propre.
N.B. : ce résultat est cohérent avec le fait que le système ne possède qu'une valeur propre non nulle .
La molécule n'étant pas animée d'un mouvement de translation le long de l'axe , on aura : .
On peut écrire les équations de déplacement des atomes de la façon suivante :

Alors, lorsque est excité, les deux atomes se déplacent avec une amplitude pondérée par le rapport de leur masse et en opposition de phase.

Représentation schématique de l'état de vibration du mode normal