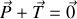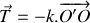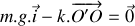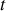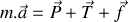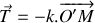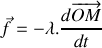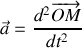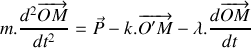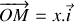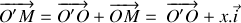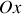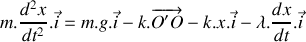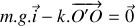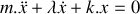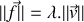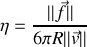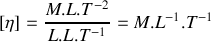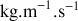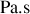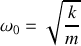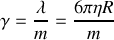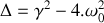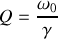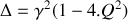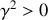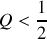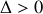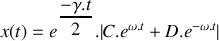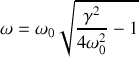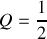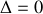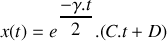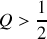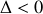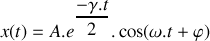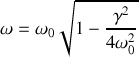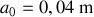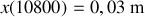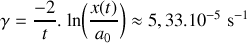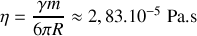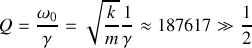Énoncé
On se propose de mesurer la viscosité
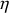de l'air en étudiant les oscillations amorties d'une bille métallique suspendue à l'extrémité d'un ressort.
La masse de la bille de rayon
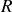est notée
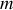. On suppose que l'air exerce une force de frottement de type fluide de norme proportionnelle à la vitesse de la bille et de sens opposé à celle-ci (
,
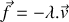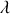est le coefficient de frottement). La poussée d'Archimède exercée par l'air sur la bille est négligée. La masse du ressort est négligeable et sa constante de raideur est notée
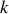. La loi de Hooke est supposée vérifiée dans tout l'exercice. On notera
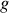l'accélération de la pesanteur.
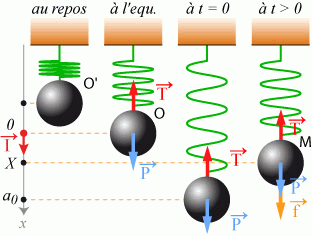
La bille est écartée verticalement de sa position d'équilibre d'une distance
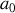, puis elle est lâchée sans vitesse initiale. Etablir l'équation différentielle gouvernant l'évolution de la position de la bille par rapport à sa position d'équilibre. Dans le cas d'une masse de forme sphérique, le coefficient de frottement
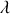s'exprime simplement comme
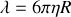(loi de Stokes). La viscosité
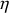s'exprime en Poiseuille.Quelle est la dimension de cette grandeur en unités MKSA ?
Réécrire l'équation différentielle obtenue à la question 1 sous la forme :
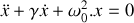et donner les expressions analytiques du taux d'amortissement
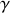et de la pulsation propre
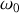en fonction de
,
,
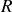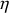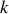et
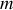.Montrer que l'équation précédente présente trois solutions distinctes et nommer les régimes auxquels celles-ci se rattachent (il n'est pas demandé de résoudre l'équation différentielle).
Si la solution de l'équation peut être approximée par :
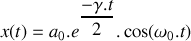, qu'en déduisez-vous pour le facteur de qualité
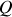de l'oscillateur ?A l'instant
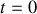, la bille a été écartée de
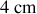de sa position d'équilibre. Au bout de 3 heures, l'amplitude maximum des oscillations est de
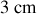. En déduire le taux d'amortissement
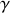, la viscosité
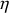de l'air et le facteur de qualité
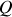de l'oscillateur. On prendra :
,
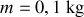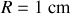et
.
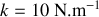