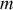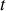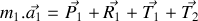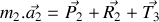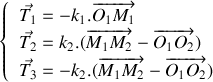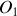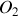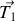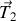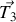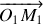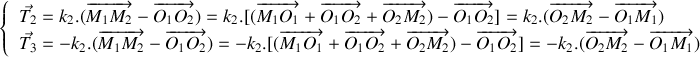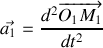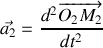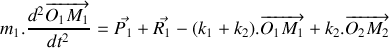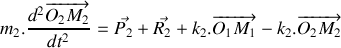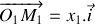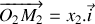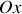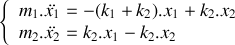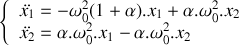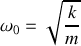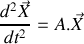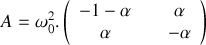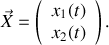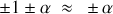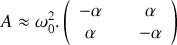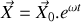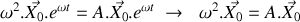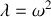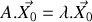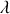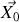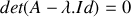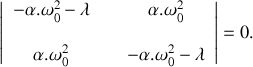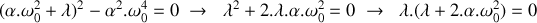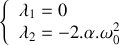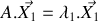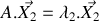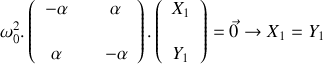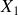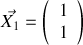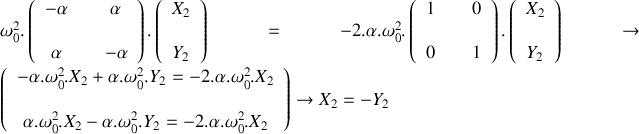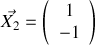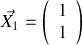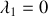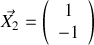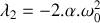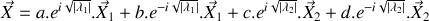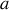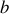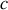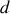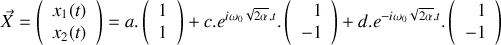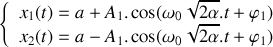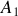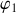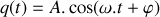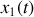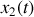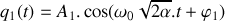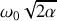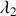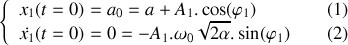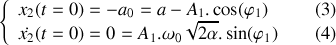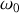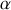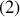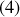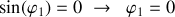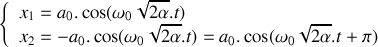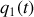Énoncé
On considère deux blocs de masses respectives
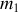et
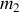liés l'un à l'autre par un ressort de constante de raideur
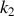. Le bloc de masse
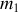est lié à un point d'ancrage fixe par l'intermédiaire d'un ressort de constante de raideur
.
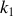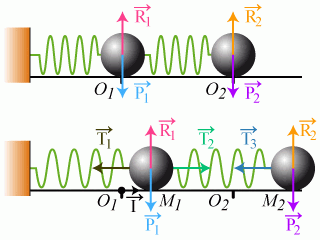
La masse des deux ressorts est négligeable et on suppose que l'amplitude de déplacement des deux blocs est toujours suffisamment faible pour que la loi de Hooke soit vérifiée. Finalement, tous les frottements sont considérés comme négligeables.
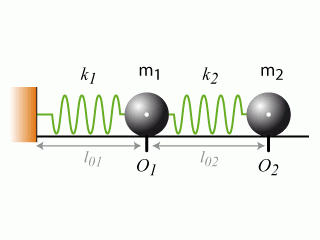
Etablir le système d'équations différentielles gouvernant l'évolution de la position des deux blocs dans le temps.
On considère désormais que les blocs sont de masse identique de sorte que
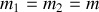. Par ailleurs, on posera
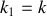et
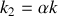. On considère également que la constante de raideur
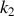est bien supérieure à
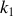de sorte que
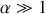. 2.a) Ecrire le système de deux équations différentielles obtenu à la question 1 sous la forme vectorielle :
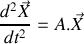. Dans la matrice
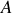, on considérera que
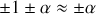. Ceci étant admis, déterminer les valeurs propres et les vecteurs propres de
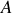. 2.b) Montrer que la solution générale du système d'équations du mouvement s'écrit sous une forme simple.
2.c) Préciser le ou les mode(s) propre(s) de vibration du système d'oscillateurs et donner la ou les pulsation(s) propre(s) de vibration du système.
A l'instant
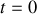, le bloc de masse
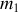est écarté d'une distance
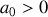de sa position d'équilibre tandis que le bloc de masse
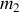en est écarté d'une distance
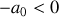. Les deux blocs sont lâchés en même temps sans vitesse initiale.Donner les lois horaires d'évolution de la position des deux blocs. Préciser la nature du ou des mode(s) propre(s) de vibration excité(s) par ces conditions initiales.
