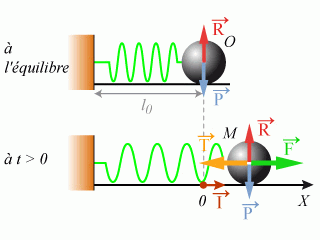
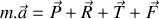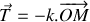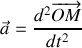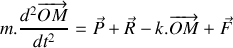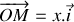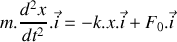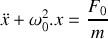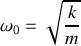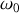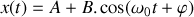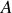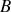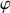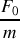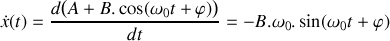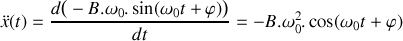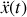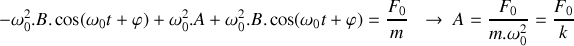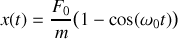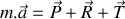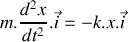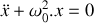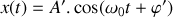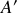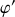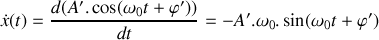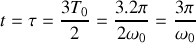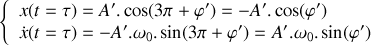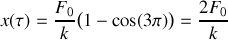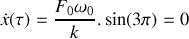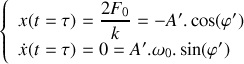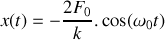Énoncé
On considère un bloc de masse
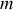 pouvant se déplacer sans frottement le long d'un support horizontal de direction
pouvant se déplacer sans frottement le long d'un support horizontal de direction
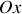 (vecteur unitaire
(vecteur unitaire
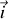 ). Il est attaché à un point d'ancrage fixe par l'intermédiaire d'un ressort de constante de raideur
). Il est attaché à un point d'ancrage fixe par l'intermédiaire d'un ressort de constante de raideur
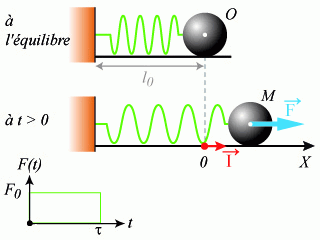
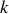 et de masse négligeable. On suppose que le déplacement du bloc est toujours d'amplitude suffisamment faible pour que la loi de Hooke soit vérifiée. A l'équilibre, le bloc se trouve en un point
et de masse négligeable. On suppose que le déplacement du bloc est toujours d'amplitude suffisamment faible pour que la loi de Hooke soit vérifiée. A l'équilibre, le bloc se trouve en un point
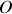 et le ressort n'est ni tendu, ni comprimé.
et le ressort n'est ni tendu, ni comprimé.
Le bloc étant initialement immobile en sa position d'équilibre, on applique brutalement une force
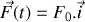 pour les temps
pour les temps
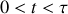 (
(
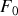 est une constante positive). L'application de cette force cesse brutalement au temps
est une constante positive). L'application de cette force cesse brutalement au temps
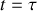 (
(
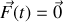 pour
pour
 , voir ci-dessous).
, voir ci-dessous).
Etablir l'équation différentielle gouvernant l'évolution de la position
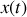 du bloc pour
du bloc pour
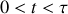 .
. Résoudre cette équation différentielle et donner la loi d'évolution
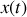 de la position du bloc pour
de la position du bloc pour
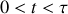 compte tenu des conditions initiales formulées précédemment.
compte tenu des conditions initiales formulées précédemment.Etablir l'équation différentielle gouvernant l'évolution de la position
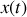 du bloc pour
du bloc pour
 .
. Les conditions initiales à
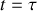 étant fournies par la loi horaire établie à la question 2, déterminer la loi d'évolution
étant fournies par la loi horaire établie à la question 2, déterminer la loi d'évolution
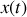 de la position du bloc pour
de la position du bloc pour
 . Pour simplifier les calculs, on fixera
. Pour simplifier les calculs, on fixera
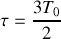 dans toute la suite (
dans toute la suite (
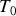 représente la période propre de l'oscillateur)
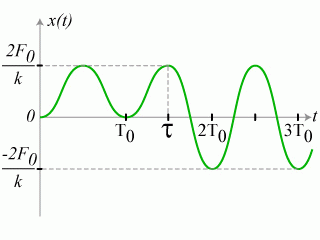
représente la période propre de l'oscillateur)Représenter schématiquement
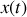 pour
pour
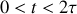 .
.