Cônes en rotation et rotations d'Euler
Ces cônes sont représentés sur les Fig. 2a et 2b. Les notations des figures sont ici conservées.
Pour assurer une identification des rotations d'Euler, il faut reconstituer le référentiel décrivant le solide.
L'analyse porte donc sur le sommet et les axes de chaque cône.
Au cours du mouvement, les deux cônes présentent tous deux un point fixe : leur sommet.
Le choix du sommet comme centre de référentiel supprime le mouvement global de translation cependant le CDM
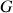effectue une rotation autour de l'axe vertical qui est le fruit des rotations du cône.
Pour faire le lien avec les deux situations respectives, a et b, il faudra faire correspondre le centre
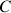des repères d'Euler avec le sommet des cônes, donc respectivement
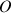et
.
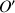Les cônes ont une symétrie de révolution à l'origine
d'un axe principal de rotation, et
de deux axes "équivalents" : le cône est une toupie symétrique.
Leur mouvement provient d'une rotation autour de leur axe principal de symétrie entraînant une rotation autour de l'axe fixe vertical.
Pour identifier les rotations d'Euler, les axes propres du cône doivent être confondus avec les axes finaux
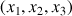et l'axe
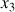est celui qui porte une des rotations : l'axe principal de symétrie (axe propre) est confondu avec
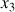. Il porte la vitesse angulaire
.
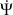La ligne nodale peut être alors associée à la génératrice instantanée qui porte le cône.
Dans le premier cas du cône reposant sur le plan
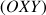, l'axe de révolution
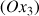portant la rotation
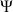est incliné d'un demi angle au sommet du cône (
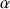) par rapport au plan
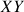et de
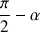par rapport à
.
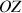Il vient alors que
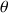est constant et vaut
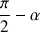. La vitesse angulaire qui lui est associée est nulle.
Dans le cas du cône dont l'axe est parallèle au plan
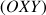, l'inclinaison
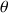vaut
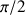et la condition de roulement sans glissement est simplifiée.
Le roulement (qui peut être sans glissement ou non) du cône posé sur le plan
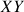produit une rotation de l'ensemble du cône autour de l'axe
.
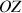Cette rotation est identifiable à la rotation d'Euler notée
.
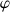De la relation entre
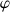et
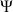peut être déduit la présence ou non de glissement et le nombre de degrés de liberté.
Ainsi en cas de roulement sans glissement, la condition liant translation du CDM et rotation propre peut être évaluée sur la distance parcourue par l'extrémité
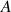de la génératrice de contact.La rotation du cône a lieu dans le sens opposé au sens trigonométrique : ceci est sans conséquence sur les équations à la condition de travailler avec des grandeurs algébriques et d'introduire les bons signes dans les applications.
