Toupie symétrique en mouvement libre
Les axes
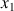et
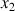sont ici toujours arbitraires du fait de la symétrie de révolution et l'axe propre (et principal) de rotation est
.
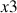Le choix des axes propres de la toupie est identique à celui de la Fig. 6, pour des raisons pédagogiques d'abord : la projection des angles d'Euler est à utiliser telle quelle.
Il en résulte que, bien que la rotation
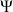existe, l'effet de la symétrie est équivalent à avoir
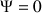dans les expressions de
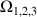tout en conservant
.
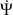En effet un calcul direct de l'énergie cinétique de rotation permet d'obtenir en posant
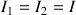, soit
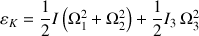et en remplaçant en fonction des angle d'Euler, d'obtenir cette énergie cinétique sous la forme :
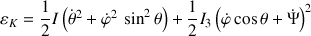
Cette dernière expression peut être assimilée aux trois vitesses angulaires distinctes suivantes :
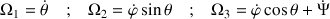
Ainsi la symétrie de la toupie permet de poser, dans les équations générales pour la vitesse angulaire,
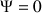tout en conservant la rotation
.
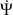Cette représentation permet de
conserver les
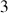directions, de conserver la rotation
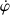dans le plan
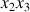et de garder la ligne nodale selon l'axe
.
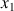Le mouvement libre de la toupie symétrique correspond à la conservation du moment cinétique total, de module et direction connus. (voir Fig. 14 où le centre
est noté
)
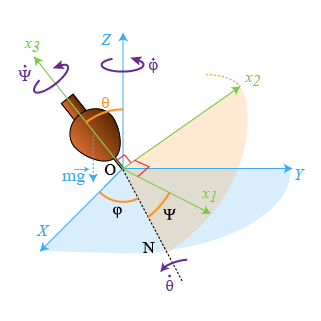
Pour rester dans les conditions de l'exemple traité dans les chapitres précédents, l'équation pour le moment cinétique s'écrit :
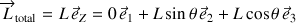
Sa forme générique est également :
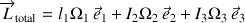
Par identification de composante à composante, les trois équations suivantes sont déduites :
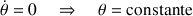
Ce qui implique une inclinaison constante de la toupie.
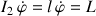
Cette vitesse de rotation est portée par l'axe vertical tout comme le moment cinétique total (soit
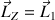) et elle est constante suite à la conservation de
. 
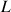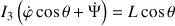
La dernière vitesse angulaire est également constante.
La seconde équation permet donc d'exprimer la vitesse de précession, soit
.
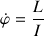Quant à la rotation autour de l'axe propre, elle peut être déduite de
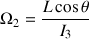et permet d'obtenir :
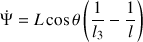
Les résultats déduits par la projection directe sont ainsi retrouvés.
Complément : Avec le formalisme lagrangien
En l'absence de pesanteur :
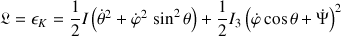
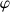Ni
, ni
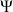n'apparaissant, les équation d'Euler - Lagrange produisent les
équations suivantes.
La variable
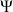est relative à la rotation selon l'axe
:
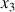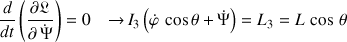
La conservation de
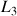implique que
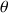est une constante.
Cette variable
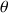, correspondant à
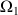, est régie par l'équation suivante :
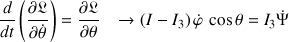
La troisième variable est
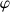et représente la rotation autour de l'axe vertical soit la précession. Son équation d'Euler - Lagrange s'écrit :
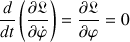
Ce qui permet de déduire la conservation du moment cinétique selon la verticale, soit :
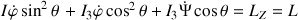
Cette dernière équation permet d'écrire
.
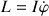Tous les ingrédients sont réunis pour retrouver les résultats précédents.
Dans le paragraphe qui suit, la formulation lagrangienne sera utilisée de manière plus... orthodoxe (impulsions conjuguées aux variables) et plus précise (pour les moments d'inertie) lorsque le poids de la toupie (situé au CDM) sera pris en compte.
Ce complément porté par le formalisme lagrangien permettra un travail comparatif avec le cas de la toupie dans le champ de pesanteur.
