Toupie et mouvement vertical
La rotation verticale de la toupie symétrique précédente, soumise à son poids, nécessite pour être stable, une vitesse de rotation
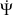minimale.
Ce mouvement est caractérisé par des axes
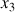et
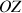confondus.
La rotation verticale (
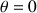) de la toupie symétrique peut être ici réalisée si la condition
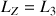est remplie.
La rotation verticale impose également
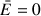: l'énergie mécanique totale vaut
.
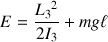De ce fait la rotation ne peut avoir lieu que si le minimum de
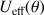est nul et se situe au voisinage de
.
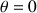Au voisinage de la position verticale, l'énergie potentielle effective est développée le plus généralement :
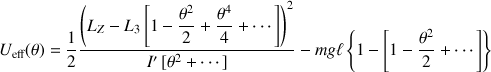
et à l'ordre dominant :
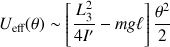
L'existence d'un minimum implique
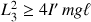ainsi qu'une vitesse de rotation minimale autour de l'axe vertical telle que
.
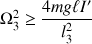Complément :
Plus généralement et dans le cas d'un mouvement gyroscopique, le calcul de l'énergie cinétique de rotation propre montre qu'elle est supérieure à l'énergie dans le champ de pesanteur.
