Mouvement d'une toupie symétrique dans le champ de pesanteur
Les notations sont précisées.
La toupie a une masse
.
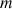Elle est symétrique : les moments d'inertie, notés
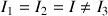, sont rapportés au centre de masse
.
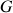Son poids
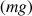est placé au centre de masse
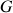, situé à la distance
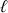sur l'axe
.
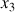Les notations angulaires précédentes sont conservées. (Fig. 15)
Les rotations ont lieu autour de la pointe
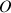de la toupie.
Les moments cinétiques qui seront utilisés sont donc rapportés au point fixe
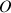de la toupie : le théorème de Huygens sera utilisé pour les moments d'inertie
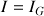pour obtenir
.
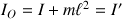Cette opération est équivalente à la décomposition de l'énergie cinétique en énergie cinétique de rotation, autour du CDM, à laquelle s'ajoute celle de translation du CDM.
Le troisième moment d'inertie reste inchangé.
Dans le cas général, la toupie est décrite par ses trois rotations.
Le formalisme lagrangien peut être utilisé pour décrire ces rotations.
La fonctionnelle de Lagrange
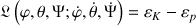dans le champ de pesanteur s'écrit :
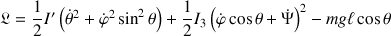
obtenue en utilisant la forme générale de l'énergie cinétique de la toupie libre.
Ainsi la différence avec cette dernière réside dans l'apparition de l'énergie potentielle de pesanteur, proportionnelle à
.
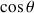Les
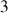degrés de liberté sont décrits par des coordonnées et des vitesses généralisées angulaires et ces grandeurs sont liées par des relations de conservation.
Notamment les équations du mouvement ou équations d'Euler-Lagrange produisent deux grandeurs conservées ou intégrales premières, utiles à toute résolution : elles réduisent la dimension du problème.
Dans le cas de la toupie symétrique, il y a en tout trois grandeurs conservées : deux moments cinétiques et l'énergie mécanique totale.
Méthode : Les lois de conservation
Le système est conservatif car il est soumis à la pesanteur, une force conservative.
Ceci produit une première loi de conservation.
1) l'énergie mécanique totale est conservée :
.
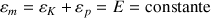Une relation entre les variables décrivant le mouvement est ainsi obtenue :
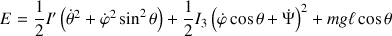
Pour exploiter cette propriété, il faut déduire les autres grandeurs conservées du formalisme lagrangien.
2) Les variables angulaires
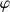et
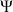sont cycliques : elles n'apparaissent pas explicitement dans l'expression du lagrangien. Les moments conjugués associés à ces variables, des moments cinétiques, sont conservés.
Ainsi est obtenue :
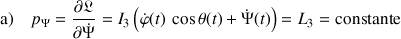
Ainsi ce moment cinétique devient à l'origine d'une contribution constante dans l'expression de l'énergie cinétique totale, par suite de l'énergie mécanique totale et du lagrangien.
En effet :
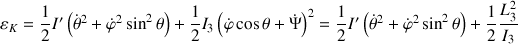
De ce fait, la rotation associée
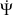joue un rôle très particulier.
La seconde grandeur conservée est issue de :
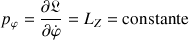
soit :
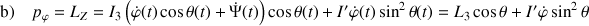
Cette loi de conservation associe la vitesse de précession à l'inclinaison de la toupie.
Ces deux grandeurs étaient déjà conservées dans le cas du mouvement libre. Mais l'utilisation de la conservation du moment cinétique totale (et de l'énergie cinétique) fixait l'angle d'inclinaison de la toupie...
L'argument justifiant
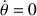n'existe plus ici.
À présent, ces grandeurs conservées,
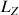et
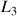, caractérisent juste les valeurs initiales en angles et vitesses angulaires des moments angulaires associés aux rotations autour des axes en indice.
Ces deux constantes sont, dans le cas général :
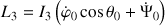
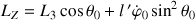
Dès à présent, et avant de pousser plus loin l'analyse du mouvement, deux pistes particulières peuvent être explorées :
La condition initiale
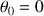produit une égalité des deux constantes :
=
.
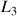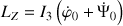Effectivement les axes
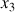et
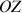sont confondus et leurs moments cinétiques égaux. Le cône est vertical et tourne avec une vitesse
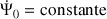. (voir le paragraphe suivant)A titre d'exercice, une analyse perturbative autour du mouvement libre et d'une inclinaison fixe de la toupie permet de dégager une description plus fine et générale de ces lois de conservation.
Toutes les constantes étant exprimées, il apparaît que l'inconnue décrivant le système est la variable
.
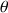L'écriture de l'équation vérifiée par cette variable est obtenue en utilisant la dernière équation d'Euler Lagrange du mouvement.
L'équation d'Euler-Lagrange correspondante s'écrit en général:
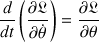
Soit pour la toupie libre :
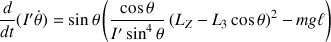
Cette équation différentielle non linéaire permet d'obtenir l'évolution au cours du temps de l'inclinaison de la toupie par rapport à la verticale, par simulation numérique.
Par ailleurs, multipliée par
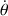, cette équation peut être intégrée pour donner une équation pour
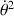, identique à celle de la conservation de l'énergie mécanique, à l'origine de l'analyse qui suit.
Pour le traitement général du mouvement de la toupie sous le champ de pesanteur, l'intégrale première "énergie mécanique" permet de déduire quelques informations sur la trajectoire de l'axe de la toupie, lequel visualise les variations de
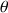au cours du temps.
Rappel de l'énergie mécanique totale.
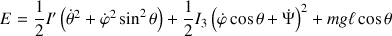
La conservation des grandeurs
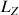et
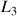permet de réduire le nombre d'inconnues, de remplacer
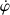et
.
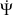Ainsi la vitesse de rotation autour de l'axe
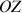peut s'écrire en fonction de la seule variable
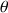selon :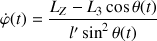
Cette rotation décrit, notamment, le mouvement de la ligne nodale.
De même, celle autour de l'axe propre
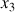s'écrit :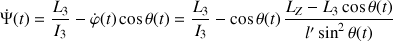
La contribution constante, dans cette dernière relation, donne un niveau moyen (ou un seuil) pour la rotation autour de l'axe de symétrie de la toupie.
L'amplitude de la variation autour de ce niveau est notamment modulée par
.
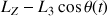L'utilisation des expressions générales des vitesses angulaires
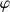et
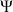en fonction de
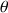dans l'expression de l'énergie mécanique totale permet de déduire l'égalité suivante :
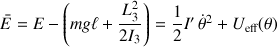
Cette écriture permet définir une énergie mécanique totale de référence
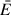autour de laquelle un schéma descriptif (graphique) peut être mis en place.
L'énergie « potentielle effective» est alors :
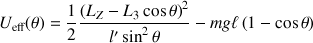
Ce potentiel représente la différence entre deux termes rigoureusement positifs.
Lorsque
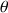tend vers
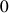ou
il tend vers +∞ . Dans cet intervalle angulaire, un angle intermédiaire devrait correspondre à un minimum d'énergie potentielle effective : au moins un minimum est donné par une représentation graphique intuitive.
Les conditions pour l'obtention d'un seul minimum en
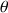s'obtiennent par l'annulation de la dérivée de l'énergie potentielle effective qui suit :
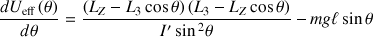
Le nombre exact d'extrema est obtenu par la résolution générale de cette équation, paramétrée par
,
,
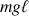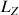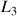et
.
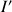Dans le cas le plus simple d'un seul minimum de l'énergie potentielle effective, lorsque la vitesse de rotation
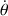est non nulle (et la rotation existe), la grandeur
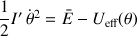doit être positive.
Ceci impose la condition
.
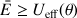L'égalité permet de déduire une équation pour
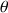qui, une fois résolue, donne deux angles limites pour le mouvement et donc une trajectoire fermée entre les deux valeurs,
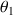et
.
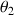Ces points de rebroussement ont déjà été visualisés graphiquement dans le problème à deux corps.
Alors que la rotation de l'axe
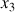autour de l'axe fixe vertical
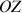décrit la précession, le mouvement de
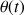, entre les deux valeurs
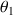et
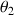, caractérise le phénomène de nutation décrivant une oscillation du plan de symétrie (plan incliné de la représentation d'Euler) autour de la ligne nodale.
Ce mouvement de l'axe
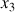est représenté sur la Fig. 16.
Le schéma de la figure décrit le mouvement de l'axe
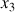sur la surface d'une sphère centrée sur la pointe de la toupie posée au sol :
La précession (rotation globale autour de l'axe vertical) est indiquée par les cercles roses, qui marquent également l'inclinaison de la toupie.
le tracé en vert décrit donc, en plus, un déplacement plus fin entre deux inclinaisons extrêmes.
La rotation selon
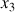respecte le sens de celle d'Euler.
Ce dernier mouvement se décline en trois différents cas de figures.
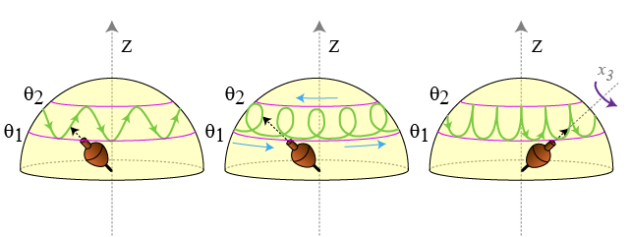
Trois types de nutation peuvent être observés entre les angles d'inclinaison limites
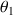et
.
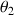Dans le cas a), le sens du mouvement est uniforme identique à celui de la précession.
Dans le cas b) le sens de la nutation change sur un des angles limites (
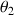sur la figure).
Le dernier cas marque la transition entre les deux situations (séparatrice).
Les différences de mouvement entre les trois types de mouvement de la Fig. 16 sont obtenues par l'analyse comparative du signe de la vitesse angulaire (
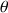) tout au long du mouvement.
Le changement de signe se produisant au voisinage d'un point de rebroussement, le calcul est effectué au voisinage de cet angle limite.
Ce changement de signe de la vitesse au cours du mouvement est porté par la relation suivante
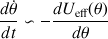, obtenue par la dérivation temporelle de
.
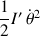Mais il est également porté par le mouvement de la ligne nodale décrit par le signe de
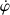qui est directement déduit de l'expression
.
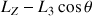