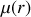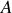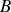Nous pouvons ainsi intégrer un champ le long d'une courbe donnée pour obtenir une valeur intégrale. Par exemple, si est la masse linéique d'un fil, en intégrant le long du fil entre deux points et nous pouvons obtenir la masse 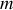du fil.

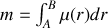
Remarquons que si la masse linéique est constante nous pouvons la sortir de l'intégrale et nous obtenons le résultat intuitif.

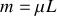
où 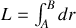 est la longueur du fil.

En général si nous considérons un champ vectoriel 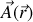l'intégrale du champ le long d'une courbe donnée 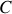sera appelée circulation 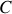du champ le long de la courbe.

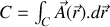
Ceci doit par exemple vous rappeler la définition du travail d'une force vue en première année. Notons que le produit scalaire est important pour bien obtenir un résultat qui soit un nombre réel ; d'autre part, si le champ est toujours perpendiculaire à l'élément de la courbe (voir le cours de géométrie des courbes correspondant) le résultat sera nul.

Figure 2: le travail nécessaire à amener le train d'un point A à un point B est égal à la circulation de la force appliquée pour ce faire.