De la même façon il est possible d'intégrer un champ vectoriel sur une surface donnée à condition qu'elle ait des propriétés de régularité convenables, ce que nous supposerons être vrai.

Ainsi si nous considérons un champ vectoriel 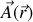l'intégrale du champ sur une surface donnée 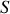sera appelée flux 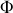du champ à travers la surface.

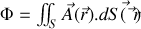
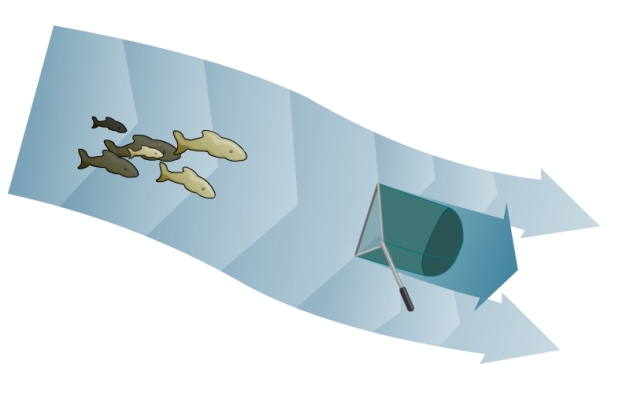
Ceci doit par exemple vous rappeler la définition du travail d'une force vue en première année. Comme pour la circulation, notons que le produit scalaire est important pour obtenir un résultat qui soit un nombre réel. On peut voir ce flux comme en mécanique des fluides, dans l'exemple d'une rivière, la quantité d'eau passant à travers une surface donnée de forme quelconque si on considère comme grandeur 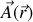la vitesse du fluide multipliée par sa masse volumique, exemple que nous reprendrons plus tard.

Figure 3: : le travail nécessaire à amener le train d'un point A à un point B est égal à la circulation de la force appliquée pour ce faire

Notons également que la présence d'un produit scalaire est importante : ainsi, dans l'exemple précédent, si on choisit une surface perpendiculaire au sens du courant, le flux est évidemment nul.