Énoncé
Une perle de masse
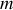 glisse sans frottement sur une tige horizontale. La tige est entraînée en rotation dans le plan horizontal, avec une vitesse angulaire constante
glisse sans frottement sur une tige horizontale. La tige est entraînée en rotation dans le plan horizontal, avec une vitesse angulaire constante
 . On supposera que le référentiel lié au sol
. On supposera que le référentiel lié au sol
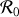 est galiléen.
est galiléen.
En utilisant le principe fondamental de la dynamique dans le repère
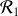 lié à la tige, déterminer l'équation du mouvement de la perle.
lié à la tige, déterminer l'équation du mouvement de la perle.Déterminer la trajectoire de la perle par rapport à la tige, puis par rapport au sol en supposant que la perle est initialement au repos à une distance
 de l'axe de rotation.
de l'axe de rotation. Déterminer la résultante de la force de contact de la tige sur la perle.
Le référentiel
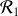 étant non galiléen, la première étape pour y appliquer le principe fondamental de la dynamique est la détermination des forces d'inertie.
étant non galiléen, la première étape pour y appliquer le principe fondamental de la dynamique est la détermination des forces d'inertie.
Pour déterminer les forces d'inertie, on peut calculer l'accélération de la perle par rapport au référentiel galiléen
 .
.
Déterminer la position de la perle dans le repère
 lié au sol, puis dans le repère tournant
lié au sol, puis dans le repère tournant
 lié à la tige.
lié à la tige.Déterminer la vitesse et l'accélération de la perle par rapport au référentiel
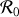 puis par rapport au référentiel
puis par rapport au référentiel
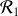 .
.En comparant les accélérations par rapport aux deux référentiels, identifier les forces d'inertie dans le repère
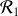 .
.Faire un bilan des forces dans le référentiel
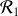 puis appliquer le principe fondamental de la dynamique pour obtenir l'équation du mouvement de la perle dans le référentiel
puis appliquer le principe fondamental de la dynamique pour obtenir l'équation du mouvement de la perle dans le référentiel
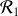 .
.
Référentiels non-galiléens. Quantité de mouvement : NLP_C_M01_G03
L'étude d'un système mécanique peut être décomposée de façon méthodique.
En premier lieu, il est nécessaire de "visualiser" le système étudié. Cela permet, outre le fait de vérifier que l'on a bien compris le système (que l'on a bien lu l'énoncé), de se faire une idée du mouvement et donc de la solution du problème. Il faudra bien entendu garder en tête cette solution tirée de notre "bon sens" pour la comparer à la solution dérivée mathématiquement des équations du mouvement.
Une fois le système bien compris, on peut se lancer dans sa modélisation.
La première étape est le paramétrage, il faut définir des repères (poser des règles physiques) qui permettront de paramétrer le système, c'est-à-dire de définir de manière univoque la position du système à l'aide de grandeurs géométriques (distances et/ou angles).
Il y a, de manière générale, plusieurs façons de décrire la position d'un système, à chacune est associé un repère (cartésien, polaire etc.). Cependant il arrive fréquemment (notamment dans le cas d'un système possédant une géométrie simple) qu'un repère rende le paramétrage plus simple.
Les lois de la dynamique (principe fondamental de la dynamique ou théorème du moment cinétique) sont définies dans des référentiels galiléens, il est donc nécessaire d'identifier parmi les différents repères que l'on a pu poser ceux pouvant constituer de tels référentiels.
Une fois cela fait, on doit identifier les différentes forces qui s'appliquent sur le système étudié puis on peut appliquer les théorèmes généraux qui conduisent à des relations vectorielles.
Soit on choisit de travailler dans un référentiel galiléen c'est-à-dire que les vitesses et les accélérations des constituants du système seront calculées par rapport à ce référentiel.
Soit on choisit de travailler dans un référentiel non-galiléen mais dans ce cas il faudra tenir compte des forces (ou pseudo-forces) d'inertie.
La dernière étape consiste à projeter la relation vectorielle obtenue dans un repère afin d'obtenir une série d'équations différentielles scalaires portant sur les paramètres du système puis de résoudre les équations (et de vérifier que la solution coïncide avec le "bon sens").
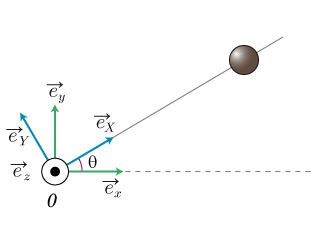
On pose
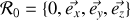 le repère cartésien fixe et
le repère cartésien fixe et
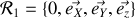 le repère tournant avec l'axe
le repère tournant avec l'axe
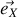 aligné avec la tige et le point
aligné avec la tige et le point
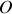 pris sur l'axe de rotation.
pris sur l'axe de rotation.
Équation du mouvement de la perle :
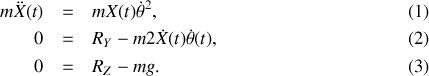
Équation horaire de la perle par rapport à la tige :
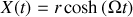 .
.Équation horaire du mouvement de la perle par rapport au sol :
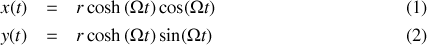
Les composantes
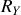 et
et
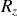 de la réaction de la tige sur la perle sont :
de la réaction de la tige sur la perle sont :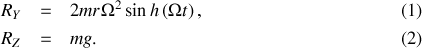
1. L'étude se fait dans le plan horizontal.
La première étape de l'étude d'un système mécanique consiste à paramétrer le mouvement en plaçant les repères (ou bases) permettant de le décrire.
Pour cela, on pose
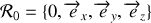 le repère cartésien et
le repère cartésien et
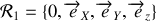 le repère tournant avec l'axe
le repère tournant avec l'axe
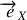 aligné avec la tige et le point
aligné avec la tige et le point
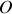 pris sur l'axe de rotation.
pris sur l'axe de rotation.
a) Position de la perle
La position de la perle P dans le repère
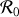 est donnée par le vecteur position :
est donnée par le vecteur position :
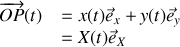
L'axe
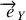 étant orthogonal à la tige, on a
étant orthogonal à la tige, on a
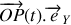 , le vecteur position n'a donc qu'une composante non nulle dans la base
, le vecteur position n'a donc qu'une composante non nulle dans la base
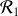 . En définissant l'angle
. En définissant l'angle
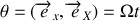 on obtient la relation de passage entre les composantes du vecteur position dans les deux repères.
on obtient la relation de passage entre les composantes du vecteur position dans les deux repères.
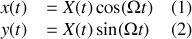

b) Vitesse et accélération de la perle par rapport au référentiel fixe
La vitesse
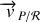 de la perle
de la perle
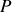 par rapport au référentiel fixe
par rapport au référentiel fixe
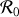 s'exprime soit dans le repère fixe
s'exprime soit dans le repère fixe
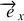 ,
,
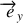 soit dans le repère tournant
soit dans le repère tournant
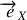 ,
,
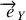 :
:
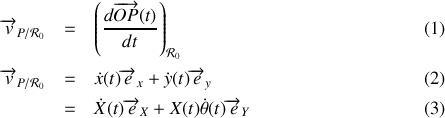
De même l'accélération
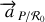 de la perle
de la perle
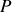 par rapport au référentiel fixe
par rapport au référentiel fixe
 s'exprime soit dans le repère fixe
s'exprime soit dans le repère fixe
 soit dans le repère tournant
soit dans le repère tournant
 :
:
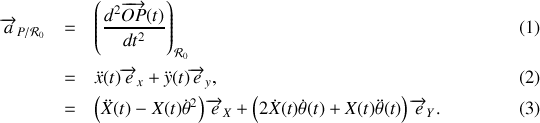
Les relations (1) et (2) permettent de faire le lien entre les expressions de la vitesse et de l'accélération exprimées dans les repères
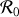 et
et
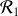 . Le choix du repère pour exprimer les vecteurs n'est qu'une convenance.
. Le choix du repère pour exprimer les vecteurs n'est qu'une convenance.
Vitesse et accélération de la perle par rapport au référentiel tournant
Vitesse et accélération de la perle par rapport au référentiel tournant sont obtenues en considérant fixes les vecteurs de base du repère
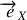 ,
,
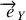 :
:
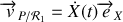
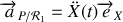
On remarque ainsi que :
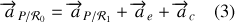
avec
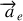 l'accélération d'entraînement et
l'accélération d'entraînement et
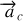 l'accélération de Coriolis. L'accélération d'entraînement
l'accélération de Coriolis. L'accélération d'entraînement
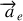 correspond à l'accélération de la perle immobile par rapport à la tige en rotation, ou encore à l'accélération du point de la tige où se trouve la perle :
correspond à l'accélération de la perle immobile par rapport à la tige en rotation, ou encore à l'accélération du point de la tige où se trouve la perle :
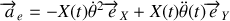 ; ici la composante sur
; ici la composante sur
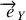 est nulle puisque la vitesse de rotation est constante, ne subsiste donc qu'une accélération centripète. L'accélération de Coriolis rassemble les termes restants
est nulle puisque la vitesse de rotation est constante, ne subsiste donc qu'une accélération centripète. L'accélération de Coriolis rassemble les termes restants
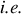
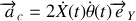 .
.
c) Identification des forces d'inertie
Le repère
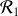 n'est pas galiléen, pour mettre en suivi le principe fondamental de la dynamique dans ce repère il faut tenir compte des forces d'inertie. En effet, en travaillant dans le repère
n'est pas galiléen, pour mettre en suivi le principe fondamental de la dynamique dans ce repère il faut tenir compte des forces d'inertie. En effet, en travaillant dans le repère
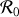 , on aurait écrit :
, on aurait écrit :
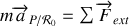
soit en utilisant (3) :
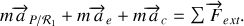
L'expression du principe fondamental de la dynamique dans le repère
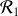 est donc :
est donc :
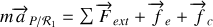
où
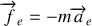 est la force d'inertie d'entraînement centrifuge et
est la force d'inertie d'entraînement centrifuge et
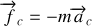 la force de Coriolis, perpendiculaire au mouvement.
la force de Coriolis, perpendiculaire au mouvement.
d) Expression du principe fondamental de la dynamique dans le référentiel
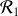
Les forces extérieures s'appliquant sur la perle sont ici le poids
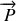 d'une part et la réaction
d'une part et la réaction
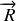 de la tige sur la perle. Finalement, on obtient l'expression du principe fondamental de la dynamique dans le repère
de la tige sur la perle. Finalement, on obtient l'expression du principe fondamental de la dynamique dans le repère
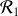
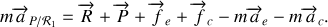
Pour projeter cette égalité vectorielle, il faut décomposer les forces extérieures dans le repère choisi. Le choix du repère
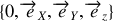 est ici tout indiqué puisque l'expression de l'accélération y est plus concise.
est ici tout indiqué puisque l'expression de l'accélération y est plus concise.
Le poids est vertical descendant, il se décompose dans le repère tournant comme
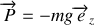 où
où
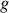 est le module de l'accélération de la pesanteur.
est le module de l'accélération de la pesanteur.
La force de réaction de la tige sur la perle n'a pas de composante dans la direction
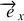 puisqu'il n'y a pas de frottement, soit
puisqu'il n'y a pas de frottement, soit
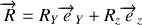 .
.
Finalement, en projetant l'expression vectorielle du principe fondamental de la dynamique dans le repère
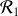 dans le repère
dans le repère
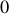 ,
,
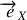 ,
,
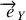 ,
,
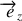 , on obtient trois égalités scalaires :
, on obtient trois égalités scalaires :
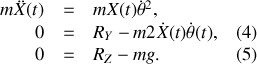
La première égalité est l'équation du mouvement, les deux autres permettent de déterminer les composantes
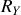 et
et
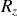 de la réaction de la tige sur la perle.
de la réaction de la tige sur la perle.
2. Étude de l'équation du mouvement
La seule force qui contribue au mouvement est la force centrifuge qui, en donnant une accélération positive à la perle, expulse la perle du centre de rotation
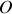 .
.
La rotation de la tige étant uniforme,
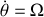 est une constante. L'équation du mouvement est une équation différentielle linéaire à coefficients constants. L'équation horaire du mouvement est donc de la forme
est une constante. L'équation du mouvement est une équation différentielle linéaire à coefficients constants. L'équation horaire du mouvement est donc de la forme
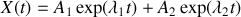
où
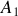 et
et
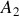 sont deux constantes qui dépendent des conditions initiales. Les constantes
sont deux constantes qui dépendent des conditions initiales. Les constantes
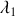 et
et
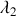 sont les zéros du polynôme caractéristique
sont les zéros du polynôme caractéristique
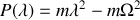 soit
soit
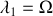 et
et
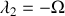 .
.
Détermination de la trajectoire
En utilisant les conditions initiales, on trouve pour la vitesse :
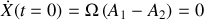 soit
soit
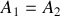 (on suppose ici
(on suppose ici
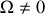 bien évidemment) et pour la position
bien évidemment) et pour la position
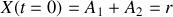 . L'équation horaire de la trajectoire de la perle par rapport à la tige est donc :
. L'équation horaire de la trajectoire de la perle par rapport à la tige est donc :
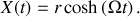
Enfin, en utilisant les relations (1) et (2), on obtient l'équation horaire du mouvement de la perle par rapport au sol :
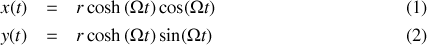
qui correspond à une spirale logarythmique.
3. Détermination de la réaction de la tige
Les composantes
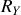 et
et
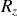 de la réaction de la tige sur la perle se déterminent par les deux égalités (4) et (5), et l'on obtient
de la réaction de la tige sur la perle se déterminent par les deux égalités (4) et (5), et l'on obtient
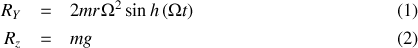
Ainsi à mesure que la perle s'écarte du centre de rotation, sa vitesse le long de la tige augmente et la réaction perpendiculaire
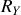 diverge.
diverge.
Il est donc en toute rigueur nécessaire de tenir compte d'éventuelles déformations de la tige sous l'effet de la force de Coriolis.



